Тема № 5Дифференциальное исчисление функции нескольких

Переменных.

 

5.1. Частные производные функции двух переменных

 

Переменная z называется функцией двух независимых переменных х и у на некотором множестве точек , если каждой паре значений 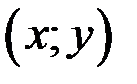из множества 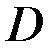соответствует определенное значение величины z.

Пишут:

.

С геометрической точки зрения функция представляет собой поверхность.

Если при 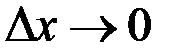отношение частного приращения функции к вызвавшему его приращению аргумента 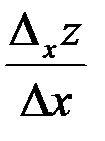имеет конечный предел, то этот предел называется частной производной функции 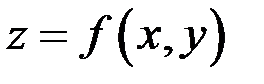по независимой переменной х в точке 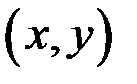и обозначается 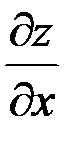, или , или .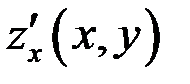

Таким образом, по определению

.

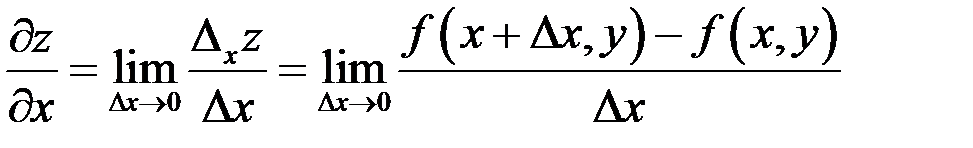Аналогично,

.

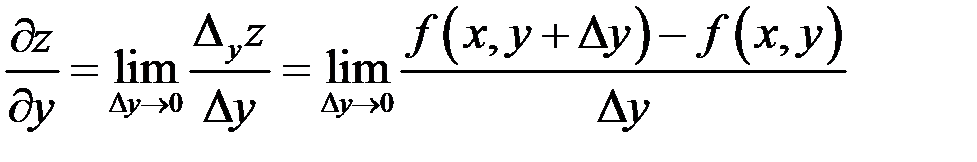Так как вычисляется при неизменном значении переменной у, а 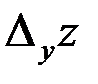– при неизменном значении переменной х, определение частных производных можно сформулировать так: частной производной по х функции 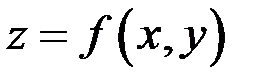называется обычная производная этой функции по х, вычисленная в предположении, что у есть постоянная; частной производной по у функции называется ее производная по у, вычисленная в предположении, что х – постоянная.

 

Пример 1

Найти частные производные функции .

Решение

 

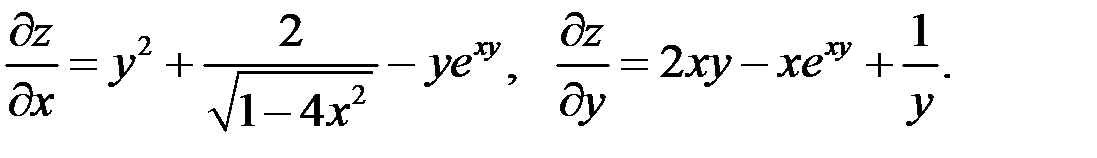
Пример 2

Показать, что функция 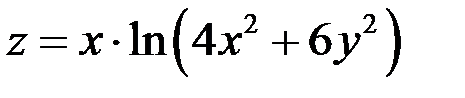удовлетворяет уравнению .

Решение

Найдем частные производные

,

.

Подставим найденные выражения в левую часть уравнения:

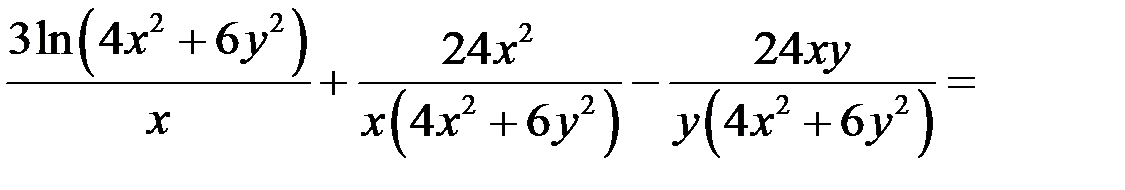
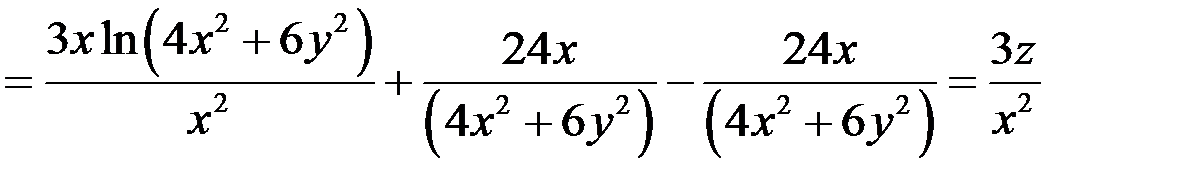что и требовалось доказать.

5.2. Дифференциал функции двух переменных

 

Частным дифференциалом функции 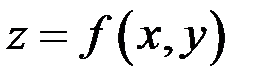называется произведение частной производной на соответствующее произвольное приращение независимой переменной:

выражение 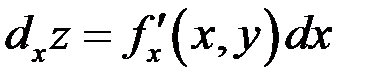называется частным дифференциалом функции 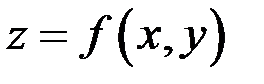по переменной х;

выражение называется частным дифференциалом функции по переменной у.

 

Пример 1

Найти частные дифференциалы функции

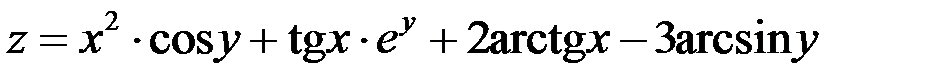
Решение

, .

 

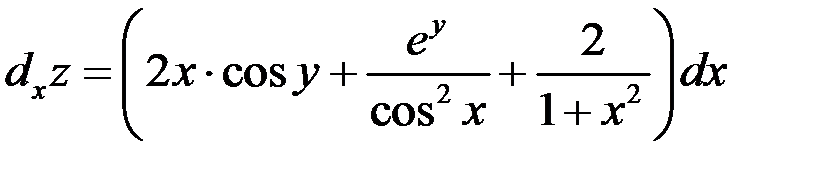Полный дифференциал функции равен сумме ее частных дифференциалов:

.

 

Пример 2

Найти дифференциал функции .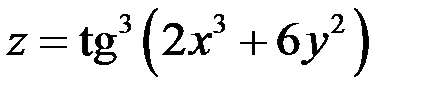

Решение

Найдем частные производные

,

.

Подставим частные производные в формулу полного дифференциала, получим

.

 

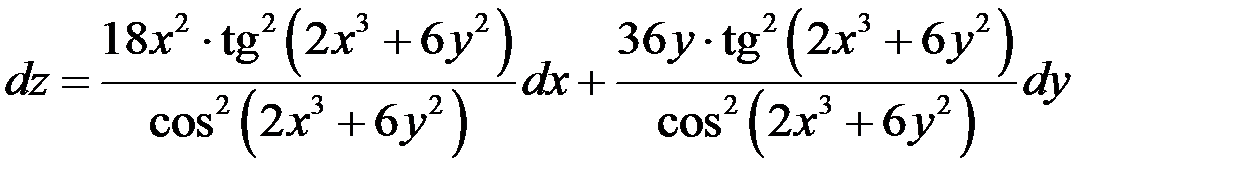Краткое содержание (программа) курса