В основе метода математической индукции лежит принцип математической индукции. Он заключается в следующем: некоторое утверждение справедливо для всякого натурального n, если оно справедливо для n = 1 и из справедливости утверждения для какого-либо произвольного натурального n = k следует его справедливость для n = k+1. То есть, доказательство по методу математической индукции проводится в три этапа: во-первых, проверятся справедливость утверждения для любого натурального числа n (обычно проверку делают для n = 1); во-вторых, предполагается справедливость утверждения при любом натуральном n=k;
в-третьих, доказывается справедливость утверждения для числа n=k+1, отталкиваясь от предположения второго пункта.
Доказательство. Предположим противное, то есть предположим, что утверждение справедливо не для всякого натурального n. Тогда существует такое натуральное m, что: 1) утверждение для n=m несправедливо, 2) для всякого n, меньшего, утверждение справедливо (иными словами, m есть первое натуральное число, для которого утверждение несправедливо). Очевидно, что m>1, т.к. дляn=1 утверждение справедливо (условие 1). Следовательно, 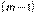 – натуральное число. Выходит, что для натурального числа утверждение справедливо, а для следующего натурального числа m оно несправедливо. Это противоречит условию 2. Заметим, что в доказательстве использовалась аксиома о том, что в любой совокупности натуральных чисел содержится наименьшее число.Доказательство, основанное на принципе математической индукции, называется методом полной математической индукции. Доказать, что при любом натуральномnчисло
– натуральное число. Выходит, что для натурального числа утверждение справедливо, а для следующего натурального числа m оно несправедливо. Это противоречит условию 2. Заметим, что в доказательстве использовалась аксиома о том, что в любой совокупности натуральных чисел содержится наименьшее число.Доказательство, основанное на принципе математической индукции, называется методом полной математической индукции. Доказать, что при любом натуральномnчисло 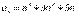 делится на 3.Решение.Воспользуемся методом полной математической индукции.
делится на 3.Решение.Воспользуемся методом полной математической индукции.
1) При n=1 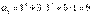 , поэтомуa1делится на 3 и утверждение справедливо приn=1 2) Предположим, что утверждение справедливо при n=k,
, поэтомуa1делится на 3 и утверждение справедливо приn=1 2) Предположим, что утверждение справедливо при n=k,  , то есть что число
, то есть что число 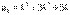 делится на 3, и установим, что приn=k+1 число
делится на 3, и установим, что приn=k+1 число 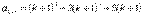 делится на 3. В самом деле,
делится на 3. В самом деле, 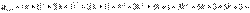
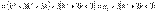
Аксиоматическое определение сложения натуральных чисел. Теорема о его существовании и единственности с доказательством. Таблица сложения.
Сложением натуральных чисел называется алгебраическая операция, обладающая свойствами: "1) (а Î N)а + 1 = а', 2) "(а, b Î N)а + b' =(а +b)'. Число а + b называется суммой чисел а и b, а сами числа а и b - слагаемыми. Как известно, сумма любых двух натуральных чисел представляет собой также натуральное число, и для любых натуральных чисел а и b сумма а +b -единственна. Другими словами, сумма натуральных чисел существует и единственна. Теорема 3. Сложение натуральных чисел существует и оно единственно.Эта теорема состоит из двух утверждений (двух теорем): сложение натуральных чисел существует; сложение натуральных чисел единственно. Доказательство единственности сложения. Допустим, что в множестве N. Для этих операций имеем:Åсуществует две операции сложения, обладающие свойствами 1 и 2. Одну из них обозначим знаком +, а другую – знаком 1) а+1=а';1) аÅ 1=а';
2) а + b ' = (а +b)' 2)а Åb' =(а Å b)'. Докажем, что если "(а, b Î N)а + b = а Å b. (1) Пусть число а выбрано произвольно, а b принимает различные натуральные значения. Обозначим через М множество всех тех и только тех чисел b, для которых равенство (1) истинно.
ÎНетрудно убедиться в том, что 1 М. Действительно, из того, что а + 1=а'= аÅ 1 следует, что а + 1 = аÅ 1. Докажем теперь, что если b Î М, то b'Î М, т.е., если а + b = а Åb, то а + b ' = а Åb'. Так как а + b= а Åb, то по аксиоме 2 (а +b)' =(а Å b)' и тогда а + b ' = (а +b)' =(а Å b)' = а Åb'. Поскольку множество М содержит 1 и вместе с каждым числом b содержит и число b', то по аксиоме 4, множество М совпадает с N, а значит, равенство (1) истинно для любого натурального числа b. Так как число а было выбрано произвольно, то равенство (1) верно при любых натуральных числах а и b, на множествеÅто есть операции + иN могут отличаться друг от друга только обозначениями. Доказательство существования сложения. Пусть М - множество тех и только тех чисела, для которых можно определить а + b Îтак, чтобы были выполнены условия 1 и 2. Покажем, что 1М. Для этого при любом b положим 1 + b = b '. (2) Тогда:1) 1 + 1 = 1'- по правилу (2), т.е выполняется равенство а + 1 = а при а = 1.2) 1 + b '= (b ')'= (1 +b)' - по правилу (2.), т.е. выполняется равенствоа + b ' = (а +b)' при а = 1. Итак, 1 принадлежит множеству М. Таблица сложения:
| a+1 | a+2 | a+3 | a+4 |
| 1+1=1‘=2 | 1+2=1+1‘=(1+1)‘ =2‘=3 | 1+3=1+ 2‘= =(1+2)‘=3‘=4 | 1+4= |
| 2+1=2‘=3 | 2+2=2+1‘= =(2+1)‘=3’=4 | 2+3=…. | 2+4= |
| 3+1=3‘=4 | 3+2=…. | 3+3=…. | 3+4= |
 2018-01-08
2018-01-08 1372
1372
