Кожній ЗЛП можна поставити у відповідність іншу здачу ЛП, яку називають двоїстою до даної.
Початкова задача - пряма або вихідна.
Пряма та двоїста задачі тісно пов’язані між собою. З розв’язку однієї можна отримати розв’язок іншої.
Розглянемо загальну ЗЛП:
F(x) = 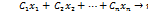 (1)
(1)
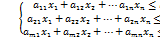 (2)
(2)
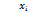 , i=
, i=  (3)
(3)
Ф(z) = 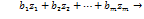 (4)
(4)
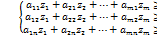 (5)
(5)
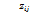 ,
, 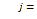 (6)
(6)
Задача(4)-(6) називається двоїстою до задачі (1)-(3)
Правила побудови взаємодвоїстих задач:
1. Одна задача повинна бути спрямованою на пошук найбільшого, а інша - найменшого значення цільової функції.
2. Обмеження задачі на мінімум повинні бути записані за допомогою ≥ і =; а в задачі на максимум – за допомогою ≤ і =.
3. Кількість змінних однієї задачі повинна бути такою самою як загальна кількість рівнянь та обмежень в системі іншої.
4. В кожній нерівності системи обмежень однієї задачі повинна відповідати невід’ємна змінна іншої задачі, а кожному рівнянню – змінна на знак якої обмежень не накладено.
5. Коефіцієнти цільової функції однієї задачі повинні бути вільними членами системи обмежень іншої.
6. Матриця коефіцієнтів системи обмежень однієї задачі повинна бути транспонованою матрицею коефіцієнтів системи обмежень іншої задачі.
Теорема(основна нерівність теорії двоїстості)
Для будь-яких допустимих розв’язків прямої задачі  ={
={ 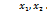 } та двоїстої
} та двоїстої 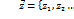
справедлива нерівність:
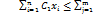 (7)
(7)
Теорема
Якщо  та
та  допустимі плани взаємодвоїстих задач та значення F(
допустимі плани взаємодвоїстих задач та значення F( ) = Ф(
) = Ф( ) (8)
) (8)
то  та
та  – оптимальні плани цих задач.
– оптимальні плани цих задач.
 2018-01-08
2018-01-08 167
167








