Якісні методи аналізу поведінки динамічних систем

 

Застосування якісної теорії до аналізу динамічних систем при вивченні соціально-економічних явищ не досить поширено та носить епізодичний характер. B основному проблемам якісного аналізу динамічних систем приділяється місце в закордонних наукових джерелах. Однак якісна теорія є ключем для розуміння складних явищ.

Завдання якісного методу — одержання якісного результату, тобто характерних рис усього явища відразу та, частково,— прогнозування явища. Математична частина якісного дослідження системи складається у зіставленні фазового портрета реальним соціально-економічним процесам або об'єктам разом із проведенням аналізу. При цьому повний якісний аналіз виникаючих систем рівнянь проводити, виявляється, немає необхідності, тому що властивості реального об'єкта встановлюють обмеження як на фазове рішення, так і на рівняння. B деяких випадках виявляється достатнім тільки знання області стійкості, положення рівноваги і їхньої економічної інтерпретації. B останні роки в якісній теорії зріс інтерес до нової якісної структури, так називаному дивному аттрактору, з яким зв'язують модель хаосу.

Розглянемо застосування якісного аналізу на прикладі.

Приклад.

Розглянемо модель росту обсягу продаж нового продукту, представленого на ринку. Для цього можна використати рівняння, загальний вид якого x'= G(x), де G(x) — нелінійна функція, що задовольняє умовам: G(O) = 0; G(b)=0; G'(x)>0 при , G'(x)<0 при , .

Тут х(t) — кількість продажів у момент часу t; b — максимально можливе значення величини, рівень насичення. Цей тип поведінки може бути досліджений за допомогою фазового графіка, тобто графіка функції, що виражає залежність x' від x. Очевидно, що графік х'=G(x), що відповідає опису, це парабола (рис. 2.1).

Значення похідної x', що відповідає деякому значенню x по рис. 2.1, збігається з тангенсом кута нахилу функції X= H(t). Намалюємо криву росту H(t) = x(t), що відповідає опису x' = G (x).

C перебігом часу x(t) зростає, тому в міру руху вправо крива H(t) (рис. 2.2) зростає. Цікавою властивістю кривої є поведінка її кута нахилу. На рис. 2.1 значення G(x) спочатку зростає від 0 до , після чого спадає до 0 у точці b. На рис. 2.2 аналогічна відповідність: збільшення G(x) означає збільшення кута нахилу дотичній H(t) зі зростанням t до точки , за точкою , де G(x) спадає, H(t) продовжує зростати, але у меншому значенні, тангенс кута нахилу дотичній зменшується. У міру того, як G(x) стає менше, наближається до 0 у крапці X = b, H(I) наближається до своєї асимптоти. Отримана крива (рис. 2.2) називається логістичною. Таким чином, виходячи із властивостей функції G(x):G(x)=ax(b - x), деа > 0; 0 < x < b; b - максимально можливе значення величини x.

Рис. 2.1. Фазовий графік об’єму продажів

 

Рис. 2.2. Крива зростання

 

Розглянемо отримане логістичне рівняння:

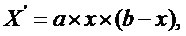(2.1)

В процесі його вирішення при початковій умові х(0) = 1, отримаємо рішення:

. (2.2)

З графіка (рис.2.2) видно, що в початкові моменти часу при t→ 0 x(t) має найбільший ріст, що практично збігається з експонентним, потім наступає період, у якому темп росту x(t) сповільнюється в міру її наближення до рівня дослідження x = b.

Дійсно, за знаком x можна визначити тип стійкості точки рівноваги.

Для розглянутого приклада система, описувана рівнянням x = ax(b - x), має рівновага x = 0 і x = b, тобто два стаціонарних рішення x = 0 і x = b.

Розглянемо точку x = 0, оскільки x ` негативно для негативних значень x, то x(t) убуває зі зміною t. Це означає, що якщо ми маємо невелике збурювання в області позитивних значень від точки рівноваги, рішення буде продовжувати віддалятися від положення рівноваги, тобто точка рівноваги x = 0 нестійка.

Далі розглянемо точку x = b. Похідна x позитивна для значень x між 0 і b і, отже, рішення x = x(t) — зростаюча функція, точка x рухається вправо по фазовій прямій у напрямку до точки рівноваги. Тому що x негативно для значень x, більших b, те x(t) убуває, і точка x рухається по фазовій прямій зі зменшенням своєї координати (уліво) до точки рівноваги. Із цих спостережень можна зробити висновок, що точка x = b — стійка. Hа рис. 2.3 ці результати представлені у графічному виді.

Таким чином, ґрунтуючись на якісному аналізі диференціального рівняння за допомогою фазового графіка й не вирішуючи його, ми одержали глибоке розуміння поводження його рішень. Якщо дано початкову умову для x, то можна впевнено сказати, як рішення x(t) буде поводитися із часом (зростати або убувати), і до якого значення воно буде сходитися.

B частковості за умови х ₀ > 0 можна зробити висновок, що x(t) буде сходитися до значення x = b.

Рис. 2.3. Характеристика стійкості ситуацій рівноваги

 

Такий аналіз дуже важливий, тому що в дійсності в економічних додатках рідко вдається знайти явне рішення нелінійних диференціальних рівнянь.

B загальному випадку якісний аналіз націлений на виявлення крапок рівноваги й умов стійкості рішень.

Формальні методи теорії стійкості і якісного аналізу динамічних систем будуть обговорюватися у розділі 3.

 

КОНТРОЛЬНІ ПИТАННЯ

 

1) У чому відмінності кількісних, якісних та структурних змін в системах?

2) Які існують механізми якісних змін?

3) У чому заклечається основна задача якісного аналізу динамічних систем?

4) Яким чином проводиться якісний аналіз?

5) Який вигляд має звичайне диференціальне рівняння? Система диференціальних рівнянь?

6) Що означає вирішення диференціального рівняння?

7) Скільки існує варіантів рішення задача Коші?

8) В чому різниця між загальним та приватним рішенням диференціального рівняння?

9) Сформулюйте теорему Коші.

10) Які виділяються види диференціальних рівнянь 1-го порядку?