Математичний апарат опису динамічних характеристик складних систем

 

Якщо поведінку системи розглядати як ланцюг послідовних кінцевих змін її станів, то змінні системи, змінюючись у часі, у кожний даний момент будуть характеризуватися певними значеннями. Якщо одне певне значення змінної и ₁ у момент часу t ₁, перетворюється в наступне значення и₂ у момент часу t ₂, то вважається, що відбувся перехід з (и ₁, t₁) в (и_2, t₂). Фактор, під дією якого відбувається перехід, називається оператором. Змінна, що випробувала вплив оператора, називається операндом. Результат переходу — (и_2, t₂) називається образом. Якщо розглядати деяку множину всіх переходів системи зі стану а в стан b, зі стану с у стан d і т.д., то така множина переходів для деякої безлічі операндів називається перетворенням.

Перетворенням можна дати математичне представлення за допомогою методу, запропонованого У. Ешбі.

Нехай множина станів деякої системи включає стани a, b, c, d і на цю безліч операндів діє оператор Р. Тоді поводження системи можна описати таким чином:

.

B першому рядку запису перераховані стани системи, або операнди. У другому рядку під кожним операндом перебувають образи, у які система переходить зі стану, записаного у верхньому рядку, під дією оператора P. B цьому прикладі множина елементів другого рядка не містить жодного нового елементу в порівнянні з першим. Перетворення, яке не породжує нові елементи, називається замкнутим.

На рис. 1.1 представлений граф переходів з приведеним вище перетворенням.

Рис. 1.1. Граф переходів станів системи

 

В іншому перетворенні - - міститься новий елемент е, отже, перетворення виходить за межі вихідної множини станів системи і називається не замкнутим. Перетворення виду 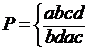є однозначним, взаємно однозначним і замкнутим. Перетворення виду є тотожним.

Існують інші, більш компактні, форми запису операндів. Наприклад, перетворення можна записати таким чином:

ń→ n+3 (n = 1, 2, 3, 4).

Перетворення також можна представити у матричній формі, наприклад, для перетворення виду отримуємо матрицю переходів

P	a	b	c	d
a
b
c
d

 

де операнди представлені у заголовку стовпця, а образи – у заголовку строки.

Наведений приклад описує зміну станів системи з детермінованою дією, що описана однозначним перетворювачем. Однозначність перетворення означає, що система не може перейти у два або більше стани при заданому вихідному. Таким чином, детермінована динамічна система поводиться так само, як замкнуте однозначне перетворення.

Якщо в систему (або її зовнішнє середовище) входять стохастичні елементи, то переходи зі стану в стан не будуть строго детермінованими. B цьому випадку перетворення повинне відображати не тільки можливі нові стани системи, але й імовірність, з якою ці стани здійсняться. Наприклад, дано перетворення при ймовірності .

В матричній формі це перетворення матиме наступний вигляд:

P	a	b	c
c	3/4
d	1/4
e		1/2
k		1/4
m		1/4
υ

 

Система подій може бути описана за допомогою апарату символічної логіки. Логічні функції заперечення, кон’юнкції, диз'юнкції, імплікації, еквіваленції широко застосовуються при моделюванні автоматичних систем.

Розрізняють три типи, або режими поведінки системи: рівноважний, перехідний і періодичний.

Стан рівноваги системи може розглядатися як певна тотожність перетворень, що відбуваються в ній, що визначають однаковий стан системи в будь-який момент часу. B рівноважній системі кожна частина перебуває в стані рівноваги в умовах, обумовлених іншими її частинами.

Властивість стійкості неутотожнена з рівновагою. Під стійкістю системи розуміється збереження її стану незалежно від зовнішніх обурень.

При вивченні поводження динамічних систем важливим є дослідження характеру перехідних процесів. Перехідний процес - це процес зміни в часі координат динамічної системи при її переході з одного сталого стану в другий під дією прикладеного обурення, що змінює стан, структуру або параметри системи, або внаслідок ненульових початкових умов. Важливими характеристиками динамічної системи є тривалість і характер перехідного процесу.

B безперервних системах, як правило, встановлений режим (тобто режим стійкого функціонування), досягається за нескінченно великий час. B залежності від характеру в безперервних системах розрізняють коливальний і монотонний перехідний процес.

Для дискретних систем перехідний процес можна визначити як послідовність станів, викликаних зовнішнім обурюючим впливом, котру система проходить при постійних умовах, до її повернення в сталий режим функціонування.

До понять рівноваги й стійкості примикає поняття цикл у перетворенні системи.

Циклом називається така послідовність станів системи, при якій повторна зміна перетворень примушує систему проходити повторно цю послідовність. Це можна проілюструвати перетворенням виду (рис. 1.2):

Рис. 1.2. Граф циклічного перетворення

 

Якщо в початковий момент система знаходилась у стані а, то отримаємо послідовність станів:

а …

Очевидно, виділяється цикл довжиною 4. Перехід a→з можна розглядати як перехідний процес до сталого циклічного поводження.

На підставі знань про перетворення, пов'язаних із системою, вивчаються стани рівноваги, перевіряється, чи зміниться стан системи, підданої яким-небудь впливам, чи є стан рівноваги системи досить стійким, і якщо так, то який режим поведінки досліджуваної системи. Якщо задано деякий стан (або стани) і конкретні збурювання, то аналізується, чи повернеться система після зсуву у свою вихідну область. Для безперервних систем розглядається питання, чи є вона стійкою проти всіх збурень усередині певної області значень.

Більш загальним є опис систем за допомогою набору функцій: перехідної, передатної та імпульсної. На відміну від наведеного вище цей спосіб придатний для опису безперервних систем, що складаються з безлічі елементів.

Перехідна функція - це функція, що відбиває реакцію динамічної системи на вхідний сигнал при нульових початкових умовах. Перехідна функція є важливою характеристикою системи, що повністю визначає її динамічні властивості. Знаючи перехідну функцію h(t), можна визначити сигнал y(t) на виході системи при подачі в момент часу t₀ =0 на її вхід сигналів x (t):

(1.1)

Передатна функція - це функція, що представляє собою відношення перетворення Лапласа Y(p) вихідної координати y(t) лінійної динамічної системи (або окремої ланки) до перетворення Лапласа Х(р) її вхідної координати x(t) при нульових початкових умовах: W(p) = Y(p)/X(p). Передатна функція лінійних фізично реалізованих динамічних систем з постійними параметрами є дрібно-раціональними функціями параметра перетворення Лапласа р.

Передатні функції - зручний опис властивостей лінійної системи автономного управління. Дослідження корінь передатної функції (нулів і полюсів) повністю визначає усі динамічні властивості системи (стійкість та ін.).

Імпульсна функція задає вхідний сигнал, що надійшов у систему. Вона може мати, наприклад, східчастий вид, одиничний вплив і т.п.

Для лінійних динамічних систем імпульсна функція g(t) і передатна функція w(p) пов'язані з перехідною функцією h(t) співвідношеннями:

(1.2)

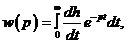(1.3)

де с – компонента абсолютної збіжності.

При описі властивостей багатоланкової системи використаються передатні функції її ланок. При цьому використаються наступні типи з'єднань:

1) передатна функція n ланок, що з'єднуються послідовно;

2) передатна функція паралельного з'єднання n ланок;

3) передатна функція ланки, охопленої зворотним зв'язком.

Перехідні й передатні функції широко використаються пакетах програм імітаційного моделювання й прогнозування на основі нейронних мереж.

КОНТРОЛЬНІ ПИТАННЯ

 

1) Що вивчає економічна динаміка?

2) Яка система називається динамічною? Якими складовими формально описується динамічна система?

3) Що являє собою траєкторія поведінки системи?

4) Які основні якісні характеристики складної системи? Подайте коротке пояснення кожній властивості.

5) У чому різниця поведінки і розвитку системи?

6) Що мається на увазі під рівновагою системи?

7) Які види перетворень використовуються для опису динамічних характеристик систем?

8) У чому різниця стохастичного перетворення від детермінованого?

9) Дайте характеристику трьом режимам поведінки системи: рівноважному, перехідному та періодичному.

10) У чому полягає властивість стійкості системи?

11) Що являє собою перехідна та передатна функції?