2018-01-08
1310
Циклом называется замкнутый маршрут в неориентированном графе. Для ориентированного графа определяется аналогично понятие контур - замкнутый путь.
Пример 3.6. В графе (рис.3.6) каждому ребру присвоен свой номер. Выделим соответствующее ему число циклов. Для нашего примера циклами Ci являются замкнутые маршруты, образованные ребрами: C1={1, 2, 5, 4}, C2={5, 6, 7}, C3={3, 6, 2}, C4={1, 2, 6, 7, 4} и т. д. Среди этих циклов найдутся такие, которые включают в себя другие циклы. Так, цикл C4 состоит из циклов C1 и C2 , у которых имеется общее ребро 5, не вошедшее в цикл 4.
Говорят, что цикл 4 получен линейной комбинацией циклов 1 и 2, т. е. является линейно зависимым от них.
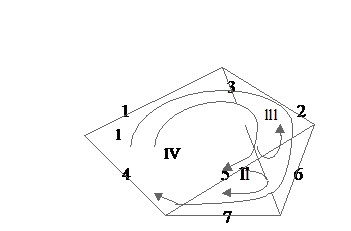
Рис. 3.6
Линейнозависимым от некоторой совокупности других циклов называется цикл, который можно построить линейной комбинацией циклов в этой совокупности.
Присвоим каждому ребру графа номер j, j=1,m и сопоставим каждому циклу Сi двоичный m- разрядный вектор Vi, компоненты vij которого определяются следующим образом: vij = 0, если ребро j не входит в цикл Ci, vij = 1 - в противном случае.
Тогда линейной комбинацией векторов Vi является результат векторной операции сложения по модулю два этих векторов.
Поскольку Vi - отношение принадлежности рёбер графа циклу Ci, а Ci - это множество рёбер, то в результате применения векторной операции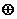 
мы получаем совокупность рёбер, входящих в циклы, составляющих линейную комбинацию за исключением общих для этих циклов рёбер.
На языке теории множеств это означает объединение множеств Ci без их пересечения, что соответствует операции «симметрическая разность» двух множеств.
| j | |||||||
| V1 | |||||||
| Å | |||||||
| V2 | |||||||
| V4 |
В нашем примере общим является ребро 5, которое исключено из цикла 4.
Линейно-независимым от совокупности других циклов называется цикл, который не может быть построен линейной комбинацией этих циклов.
Максимальное множество линейно-независимых циклов образует систему независимых циклов; мощность g этого множества называется цикломатическим числом. Это число определяется по формуле Эйлера
g=m-n+p (3.2)
3.5. Дерево. Остов
Деревом называется конечный связный граф без циклов. Из свойств отсутствия циклов и связности следует, что у дерева количество компонент связности p =1 и цикломатическое число g =0, т.е. g= m - n+ 1 =0,
отсюда следует, что
m=n -1, (3.3)
т. е. число ребер в дереве на единицу меньше числа вершин.
Ниже на рис. 3.7 приведены примеры деревьев.
Пример 3.7.
 |
Рис. 3.7
Остов - это подграф (частичный граф), который может быть построен из графа удалением некоторых ребер и который является деревом.
В общем случае для графа можно построить несколько остовов. Для приведенного ниже графа построен один из возможных вариантов остова.
Пример 3.8.
 |
Рис. 3.8
Для несвязного графа рассматриваются отдельные его компоненты. Остов такого графа - совокупность его компонент.
Пример 3.9.
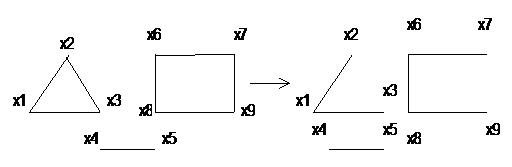
Рис. 3.9
