Примеры решения задач при помощи перебора с возвратом

Рассмотрим использование перебора с возвратом при решении других задач. Если пространство перебора представляет собой X 1  X 2  X_n, то общую схему можно записать так:

procedure перебор_с_возвратом(m: integer); var i: integer; begin if m > n then <найдено решение> else for i  X_m do begin x[m]:= i; if <x[m] совместимо с x[1],...,x[m-1]> then перебор_с_возвратом(m+1); end ; end ;

Первая задача – очень известная задача о раскраске карты (математики предпочитают обычно говорить о раскраске вершин графа).

Задача 3 Раскраска карты. Имеется географическая карта, на которой расположено n стран. Каждую страну надо раскрасить в один из k цветов так, чтобы соседние страны были раскрашены в разные цвета.



Географическую карту будем задавать в виде матрицы C размером n  n. Элемент C_i,j равен 1, если страны i и j – соседние и равен 0 иначе.

Пространство перебора состоит из наборов (x 1 ,...,x_n), x_i  {1, ...,k }. Условие совместимости m -го элемента с предыдущими: если C_i,m= 1 (1  i < m), то x_i  x_m.

Рекурсивная процедура, осуществляющая перебор с возвратом запишется по рассмотренной схеме:

procedure перебор_с_возвратом(m: integer); var i: integer; begin if m > n then <найдено решение> else for i:= 1 to k do begin цвет[m]:= i; if <цвета стран 1,...,m-1 соседних с m -ой не i> then перебор_с_возвратом(m+1); end; end;

Однако в отличие от задачи о ферзях, в данной задаче перебор можно сократить ещё больше за счёт симметрии решений задачи. Предположим, мы нашли решение задачи. Если мы теперь в этом решении у всех вершин поменяем местами i -ую и j -ую краску, то получившаяся раскраска тоже будет решением. Из таких симметричных решений нам достаточно найти одно. Таким образом, при выборе краски для очередной страны нам достаточно перебрать все уже используемые краски и всего одну (первую) из новых.

procedure перебор_с_возвратом(m: integer); var i: integer; begin if m > n then <найдено решение> else begin for i:= 1 to кол_красок do begin цвет[m]:= i; if <цвета стран 1,...,m-1 соседних с m -ой не i> then перебор_с_возвратом(m+1); end; if кол_красок < k then begin кол_красок:= кол_красок+1; цвет[m]:= кол_красок; перебор_с_возвратом(m+1); кол_красок:= кол_красок-1; end; end; end;

Задача 4 Укладка рюкзака. Из заданных n предметов выбрать такие, чтобы их суммарная стоимость была не менее чем S, а суммарный объём не превосходил V.

Мы немного видоизменили стандартную формулировку этой задачи. Обычно требуется выбрать предметы, чтобы стоимость была максимальной. В нашей формулировке задача несколько упрощена. (это упрощение непринципиально).

Стоимости предметов будут храниться в массиве стоимость, а объёмы – в массиве объём. Пространством перебора в данном случае будут все подмножества множества {1 ,...,n }. Каждое подмножество можно задавать набором (x 1 ,...,x_n), x_i  {0,1}. Теперь задачу можно переформулировать в следующем виде: Найти набор (x 1 ,...,x_n), x_i  {0,1}, такой что:
 _i= 1 ,...,n x_i· стоимость_i  S,  _i= 1 ,...,n x_i· объём_i  V.

Условия, которые можно проверять при выборе:

• суммарный объём уже выбранных предметов не превосходит V;
• суммарная стоимость выбранных предметов и тех, которые мы можем выбрать не меньше S.

Второе условие удобнее переписать в виде: суммарная стоимость невзятых предметов не превосходит стоимости всех предметов минус S. Cтоимость всех предметов минус S будем хранить в переменной доп_ост. Получаем следующий алгоритм:

procedure перебор_с_возвратом(m: integer); var i: integer; begin if m > n then <найдено решение> else begin x[m]:= 0; ост_стоимость:= ост_стоимость+стоимость[m]; if ост_стоимость <= доп_ост then перебор_с_возвратом(m+1); ост_стоимость:= ост_стоимость-стоимость[m]; x[m]:= 1; сумм_объём:= сумм_объём+объём[m]; if сумм_объём <= V then перебор_с_возвратом(m+1); сумм_объём:= сумм_объём-объём[m]; end; end;

Задача 5 Расстановка знаков. Дано целое число m. Вставить между некоторыми цифрами 1, 2, 3, 4, 5, 6, 7, 8, 9, записанными именно в таком порядке, знаки ``+'' и ``-'' так, чтобы значением получившегося выражение было число m. Например, если m= 122, то подойдёт выражение: 12+34-5-6+78+9. Если расставить знаки требуемым образом невозможно, сообщить об этом.

Решение. Приводимая в [3] программа осуществляет полный перебор вариантов. Причём даже построение выражения осуществляется для каждого варианта отдельно – т.е. самым неэффективным способом. Приведём такой вариант решения (немного улучшенный по сравнению с версией в [3]).

program signs1; var i, ii, kod: integer; t: string; op: char; s,r,m: longint; begin readln(m); { полный перебор вариантов } for ii:= 0 to 6560 do begin { построение выражения } kod:= ii; t:= '1'; for i:= 2 to 9 do begin case (kod mod 3) of 1: t:= t+'+'; 2: t:= t+'-'; end; t:= t+chr(48+i); kod:= kod div 3 end ; { вычисление результата } t:= t+'.'; s:= 1; r:= 0; op:= '+'; for i:= 2 to length(t) do begin if t[i] < '0' then begin if op = '+' then r:= r+s else r:= r-s; s:= 0; op:= t[i]; end else s:= s*10+(ord(t[i])-48) end; { проверка равенства } if r=m then writeln(t) end; end .

Если основной цикл представить несколькими вложенными циклами – каждый для отдельной позиции знака в строке, то получится 8 вложенных циклов. Тогда уже можно начинать строить выражение сразу для группы вариантов. На самом нижнем (и наиболее часто исполняемом, а значит и наиболее дорогом) уровне перебора уже нет операций построения строки – они делаются раньше – сразу для групп элементов. Получим следующий текст (строка на первом уровне – t1, на втором – t2 и т.д.):

for i2:= 1 to 3 do begin case (i2 mod 3) of 1: t2:= t1+'+'+'2'; 2: t2:= t1+'-'+'2'; else t2:= t1+'2'; end; for i3:= 1 to 3 do begin case (i3 mod 3) of 1: t3:= t2+'+'+'3'; 2: t3:= t2+'-'+'3'; else t3:= t2+'2'; end; ...

И так 8 циклов. Довольно длинно, но более эффективно. Причём рекурсивный вариант этого алгоритма устраняет громоздкость текста:

procedure sign_choice2(n: integer; var t: string); var tnew: string; i: integer; begin if n <= 9 then for i:= 1 to 3 do begin case i of 1: tnew:= t+'+'+chr(48+n); 2: tnew:= t+'-'+chr(48+n); else tnew:= t+chr(48+n); end; sign_choice2(n+1,tnew); end else begin { вычисление результата } t:= t+'.'; s:= 1; r:= 0; op:= '+'; for i:= 2 to length(t) do begin if t[i] < '0' then begin if op = '+' then r:= r+s else r:= r-s; s:= 0; op:= t[i]; end else s:= s*10+(ord(t[i])-48) end; { проверка равенства } if r=m then writeln(t) end end ;

(Вызов данной процедуры заменяет в программе signs1 весь основной цикл.)

Теперь цикл, перебирающий три варианта расстановки знаков, проще расписать напрямую следующим образом:

tnew:= t+'+'+chr(48+n); sign_choice(n+1,tnew); tnew:= t+'-'+chr(48+n); sign_choice(n+1,tnew); tnew:= t+chr(48+n); sign_choice(n+1,tnew);

Теперь осуществим самое важное улучшение алгоритма: не только построение выражения, но и подсчёт результата будем выполнять как можно раньше:

procedure sign_choice3(s,r: longint; op: char; n: integer; t: string); var newr: longint; begin if op = '+' then newr:= r+s else newr:= r-s; if n <= 9 then begin sign_choice3(n,newr,'+',n+1,t+'+'+chr(48+n)); sign_choice3(n,newr,'-',n+1,t+'-'+chr(48+n)); sign_choice3(s*10+n,r,op,n+1,t+chr(48+n)); end else { проверка равенства } if newr=m then writeln(t) end ;

И, наконец, последнее, уже не столь существенное улучшение. Раз построенное выражение (символьную строчку t) мы не используем для вычисления результата, то можно её вообще не строить (правда, запоминать расставленные знаки всё же придётся, чтобы можно было выдать результат).

program signs4; var t: array[2..9] of string; procedure sign_choice4(s,r: longint; op: char; n: integer); var newr: longint; begin if op = '+' then newr:= r+s else newr:= r-s; if n <= 9 then begin t[n]:= '+'; sign_choice4(n,newr,'+',n+1); t[n]:= '-'; sign_choice4(n,newr,'-',n+1); t[n]:= ''; sign_choice4(s*10+n,r,op,n+1); end else { проверка равенства } if newr=m then begin for i:= 2 to 9 do write(i-1,t[i]); writeln('9'); end; end; begin readln(m); sign_choice4(1,0,'+',2); end.

Итак, мы пришли всё к той же схеме перебора с возвратом. Правда в этой задаче не удаётся отсечь варианты на ранних этапах перебора (поэтому перед рекурсивным вызовом нет оператора if) и есть еще одно непринципиальное отличие – цикл заменён на три последовательных рекурсивных вызова.

Время выполнения программы, приведенной в [3] – 2.42 сек., программы signs1 – 2.20 сек., программы с процедурой sign_choice2 – 0.96 сек., программы с процедурой sign_choice3 – 0.22 сек., программы signs4 – 0.11 сек. Таким образом, нам удалось значительно сократить перебор. Да и текст программы стал короче.



Задача 6 Минимальный путь. На рисунке изображен треугольник из чисел:

7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

Требуется вычислить наименьшую сумму чисел на пути от верхней точки треугольника до основания. При этом:

• каждый шаг шаг на пути может осуществляться вниз и влево или вниз и вправо,
• число строк в треугольнике больше 1 и меньше 100,
• треугольник составлен из целых чисел от 0 до 99.

Решение. При решении задачи полным перебором число вариантов равно 2 ^n- 1, где n – число строк в треугольнике. Это, конечно же, неприемлимо. Но как сократить перебор? Трудно придумать условие, по которому мы могли бы отсекать частично построенные варианты.

Решение даёт группирование вариантов. Все пути от вершины к основанию, проходящие через некоторую промежуточную точку, объединим в одну группу. Ясно, что проверять на минимальность надо только те пути, которые от вершины до промежуточной точки проходят минимальным путём.

Теперь можем использовать то, что каждый путь проходит через одну из точек каждой из строк. Таким образом, можем последовательно разбивать все пути на две группы (в соответствие со второй строкой), потом на три (в соответствие с третьей строкой) и т.д. В каждой строке для каждой точки находим минимальный путь. В результате мы найдём минимальный путь до каждой из точек основания. После этого надо будет выбрать из них минимальный.

Пусть a_i,j означает j -ое число в i -ой строке, s_i,j – наименьшую сумму чисел от вершины до числа a_i,j. Для s_i,j выполняются следующие соотношения:

s 1,1 = a 1,1, si, 1 = ai, 1 + si- 1,1, si,i = ai,i + si- 1 ,i- 1,

si,j = ai,j + min { si- 1 ,j,si- 1 ,j- 1}, 1 < j < i  n

Теперь написать программу нетрудно. Перебор в такой программе будет совсем небольшим (только выбор минимального из двух чисел для каждого числа в треугольнике и выбор минимального из n для путей из вершины к разным точкам основания).



Приведём еще один пример – задачу, в которой удаётся полностью избежать перебора.

Задача 7 Бал. Во время бала в зале, имеющем форму M -угольника A 1 A 2 ...A_M, этикетом предписано размещаться N придворным дамам вдоль стен и в углах так, чтобы у всех стен стояло равное число дам. Если дама находится в углу, то она считается стоящей у обеих стен этого угла. Вдоль стены может размещаться любое количество дам, а в углу не больше одной. Найти требуемое расположение дам.

Решение. Первый приходящий в голову способ решения для данной задачи – перебор. Однако легко догадаться, что по-существу важно получить какую-либо расстановку дам с суммарным количеством дам, стоящих вдоль стен, кратным количеству стен. Распредилить же потом их поровну не составит труда. А суммарное количество дам, стоящих вдоль стен, (при фиксированных количестве стен и дам) зависит только от того, сколько дам стоит в углах. Оно минимально, если в каждом углу стоит по даме и максимально, если вообще ни в одном углу не стоят дамы. Точнее (обозначим это число через s): N  s  N+M. Нам требуется так подобрать s, чтобы оно было кратно M. Среди чисел от N до N+M хотя бы одно такое число обязательно найдётся. Это N+M - (N mod M). В углах будет стоять M- (N mod M) дам. Ос

 

.1 Отсечение лишних вариантов

Первый принцип при таком подходе предельно прост – не рассматривать те варианты, которые не могут дать решение задачи. Как правило, большую часть таких вариантов можно избежать, организовав перебор соответствующим образом. Часто ``лишние'' варианты не продиктованы смыслом задачи, а возникают из-за способа организации перебора. Действительно, часто используемый способ получения простых формулировок – грубо (``с запасом'') описывает пространство решений задачи. При этом структура алгоритма поиска решения становится наиболее простой – как правило, это вложенные циклы. Но ценой этому – расширение пространства перебора. Пространство перебора может быть излишне расширено и просто из-за неподходящей, неумело подобранной формулировки. Так, переходя в разобранной задаче о шашках от первой формулировки к последующим, мы по-существу убирали из рассмотрения лишние варианты (например, варианты, содержащие два одинаковых хода подряд). Сейчас же остановимся на случае, когда пространство перебора уже не удаётся сократить принципиально – получив новую формулировку, но можно исключать отдельные элементы.

Рассмотрим задачу о расстановке n ферзей.

Задача 2 N ферзей. На шахматной доске размером n  n требуется расставить n ферзей, так, чтобы они не били друг друга.



Построим замкнутую формулировку этой задачи. Позицию будем записывать в виде набора, состоящего из координат x, y всех ферзей. Условие x_i  x_j (y_i  y_j) означает то, что i -ый и j -ый ферзи стоят на разных вертикалях (горизонталях). Условия x_i+y_i  x_j+y_j и x_i-y_i  x_j-y_j означают что i -ый и j -ый ферзи не стоят на одной диагонали. Получаем следующую замкнутую формулировку: Найти набор (x 1 ,y 1 ,x 2 ,y 2 ,...,x_n,y_n), x_i, y_i  {1 ,...,n }, такой что: x_i  x_j, y_i  y_j, x_i+y_i  x_j+y_j, x_i-y_i  x_j-y_j для всех i, j  {1 ,...,n }. Заметим, что среди координат x ферзей x 1 ,x 2 ,...,x_n ровно один раз встречается каждое из чисел 1,2 ,...,n. Таким образом, достаточно перебирать только координаты y. Номера же ферзей можно рассматривать как координаты x. Итак, переформулируем задачу: Найти набор (y 1 ,y 2 ,...,y_n), y_i  {1 ,...,n }, такой что: y_i  y_j, i+y_i  j+y_j, i-y_i  j-y_j для всех i, j  {1 ,...,n }.

Нарисуем пространство для n= 3 (это слишком небольшое число для данной задачи и в этом случае вообще нет решения, но нам важно понять, что представляет из себя пространство перебора). Пространство перебора – множество {(y 1 ,y 2 ,y 3): y 1 ,y 2 ,y 3  {1,2,3}}. На рисунке элементы пространства перебора отмечены точками.

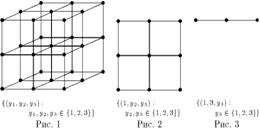
Напрашивающийся алгоритм перебора состоит в последовательном переборе сначала (т.е. на верхнем уровне перебора) трёх плоскостей, потом – прямой на плоскости (см. рисунок 2) и наконец – точки на прямой. Каждый уровень перебора соответствует перебору положения для одного ферзя.

В общем случае такой алгоритм состоит в последовательном переборе сначала положения для первого ферзя, после каждого выбора такого положения – в переборе положения для второго ферзя и т.д. Алгоритм записывается с помощью n вложенных циклов:

for i1:= 1 to n do begin ферзь[1]:= i1; for i2:= 1 to n do begin ферзь[2]:= i2; for i3:= 1 to n do begin ферзь[3]:= i3;...... <проверка построенной позиции> end ; end ; end ;

Приведённый алгоритм типичен. Пространство перебора часто состоит из наборов элементов и те значения, которые может принимать каждый элемент, перебираются последовательно – после выбора значения для одного элемента перебираются все возможные значения для следующего и т.д.

Таким образом, пространство перебора всегда – параллелепипед. (В общем случае – множество наборов {(y 1 ,...,y_n): y 1  Y 1, y_n  Y_n }, Y 1 ,..., Y_n  Y.) Такое пространство можно задать, задав множества Y 1 ,..., Y_n. В нашем случае это означает, что мы должны указать, какие значения разрешены для каждого из ферзей. Так мы приходим к компактному представлению пространства перебора, с которым и будем работать в дальнейшем.

На рисунках 4, 5, 6 показаны те же пространства перебора, что и на рисунках 1, 2, 3 соответственно. Там, где значение для ферзя запрещено – квадрат изображён чёрным цветом, где разрешено – белым. В дальнейшем мы будем вертикали, соответствующие ферзям изображать вплотную (у нас получится шахматная доска).

Проследим, какими будут первые полностью построенные позиции при приведённом алгоритме. Сначала будет рассмотрен вариант, когда все ферзи занимают положение 1, потом последний ферзь займёт положение 2 и т.д. Но постойте! Ведь уже когда первый ферзь занимает положение 1, то все позиции, в которых второй ферзь занимает положение 1 или 2 будут заведомо неприемлемы. Т.о. первые 2 · n^n- 2 вариантов будут рассмотрены впустую. Но ведь это можно было заметить уже при расстановке второго ферзя.

Иначе говоря, из пространства перебора заведомо можно удалить варианты, когда второй ферзь занимает положение 1 или 2. Для случая n= 3 сокращённое пространство перебора показано на рис. 3.

Такое сокращение можно реализовать проверкой совместимости положения выбираемого ферзя с выбранными ранее. Улучшенный алгоритм будет выглядеть следующим образом. (Мы специально не приводим конкретный алгоритм, который будет немного более эффективным, а записываем алгоритм в общей форме, которая подойдёт и для решения других задач).

for i1:= 1 to n do begin ферзь[1]:= i1; for i2:= 1 to n do begin ферзь[2]:= i2; { проверка частично построенной позиции } if <ферзь[2] не бьёт ферзь[1]> then for i3:= 1 to n do begin ферзь[3]:= i3; { проверка частично построенной позиции } if <ферзь[3] не бьёт предыдущих> then for i4:= 1 to n do begin ... if <ферзь[n] не бьёт предыдущих> then <решение найдено> end ; end ; end ; end ;

Понятно, что очень важно отсечь ненужные варианты на наиболее ранних этапах перебора. При этом мы по-существу отсекаем сразу группу ``лишних'' вариантов.

При сокращении пространства перебора надо иметь в виду насколько сокращается пространство и соотносить размер этого сокращения с затратами на его реализацию. Если размер сокращения не велик по сравнению с общим объёмом перебора, то обычно не стоит ``городить огород'' и реализовывать такое сокращение, так как затраты на выполнение более сложной схемы перебора могут ``съесть'' весь выигрыш от сокращения. Кроме того, каждое усложнение алгоритма – лишняя возможность сделать ошибку.