Для увеличения скорости подбора ключа используется распараллеливание вычислений. Существует два подхода к распараллеливанию:
§ Первый подход — построение конвейера. Пусть алгоритм соотношения 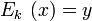 можно представить в виде цепочки простейших действий (операций):
можно представить в виде цепочки простейших действий (операций): 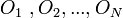 . Возьмём
. Возьмём 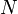 процессоров
процессоров 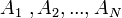 , зададим их порядок и положим, что
, зададим их порядок и положим, что 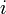 — ый процессор выполняет три одинаковые по времени операции:
— ый процессор выполняет три одинаковые по времени операции:
1. приём данных от 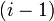 — го процессора;
— го процессора;
2. выполнение операции 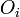 ;
;
3. передача данных следующему 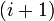 -му процессору.
-му процессору.
Тогда конвейер из 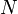 последовательно соединённых, параллельно и синхронно работающих процессоров работает со скоростью
последовательно соединённых, параллельно и синхронно работающих процессоров работает со скоростью 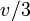 , где
, где 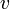 — скорость выполнения одной операции одним процессором.
— скорость выполнения одной операции одним процессором.
§ Второй подход состоит в том, что множество 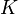 всех возможных ключей разбивается на непересекающиеся подмножества
всех возможных ключей разбивается на непересекающиеся подмножества 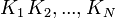 . Система из
. Система из 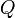 машин перебирает ключи так, что
машин перебирает ключи так, что 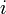 — ая машина осуществляет перебор ключей из множества
— ая машина осуществляет перебор ключей из множества 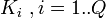 . Система прекращает работу, если одна из машин нашла ключ. Самое трудное — это разделение ключевого множества. Но если каждый процессор начнёт вычисление с какого-то произвольного ключа, то время нахождения увеличится, а схема значительно упростится. Среднее число шагов в этом случае составляет
. Система прекращает работу, если одна из машин нашла ключ. Самое трудное — это разделение ключевого множества. Но если каждый процессор начнёт вычисление с какого-то произвольного ключа, то время нахождения увеличится, а схема значительно упростится. Среднее число шагов в этом случае составляет 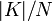 , где
, где 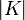 — число элементов во множестве ключей, а
— число элементов во множестве ключей, а 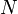 — число процессоров.
— число процессоров.
Радужные таблицы
Радужная таблица создается построением цепочек возможных паролей. Каждая цепочка начинается со случайного возможного пароля, затем подвергается действию хеш-функции и функции редукции. Данная функция преобразует результат хеш-функции в некоторый возможный пароль (например, если мы предполагаем, что пароль имеет длину 64 бита, то функцией редукции может быть взятие первых 64 бит хеша, побитовое сложение всех 64-битных блоков хеша и т. п.). Промежуточные пароли в цепочке отбрасываются и в таблицу записываются только первый и последний элементы цепочек. Создание таких таблиц требует больше времени, чем нужно для создания обычных таблиц поиска, но значительно меньше памяти (вплоть до сотен гигабайт, при объеме для обычных таблиц в N слов для радужных нужно всего порядка N2/3). При этом они требуют хоть и больше времени (по сравнению с обычными методами) на восстановление исходного пароля, но на практике более реализуемы (для построения обычной таблицы для 6-символьного пароля с байтовыми символами потребуется 2566 = 281 474 976 710 656 блоков памяти, в то время как для радужной — всего 2566·⅔ = 4 294 967 296 блоков).
Для восстановления пароля данное значение хеш-функции подвергается функции редукции и ищется в таблице. Если не было найдено совпадения, то снова применяется хеш-функция и функция редукции. Данная операция продолжается, пока не будет найдено совпадение. После нахождения совпадения цепочка, содержащая его, восстанавливается для нахождения отброшенного значения, которое и будет искомым паролем.
В итоге получается таблица, которая может с высокой вероятностью восстановить пароль за небольшое время.
Пример продолжительности подбора паролей
В таблице представлено оценочное время полного перебора паролей в зависимости от их длины. Предполагается, что в пароле могут использоваться 36 различных символов (латинские буквы одного регистра + цифры), а скорость перебора составляет 100 000 паролей в секунду.[1]
| Кол-во знаков | Кол-во вариантов | Стойкость | Время перебора |
| 5 бит | менее секунды | ||
| 10 бит | менее секунды | ||
| 46 656 | 15 бит | менее секунды | |
| 1 679 616 | 21 бит | 17 секунд | |
| 60 466 176 | 26 бит | 10 минут | |
| 2 176 782 336 | 31 бит | 6 часов | |
| 78 364 164 096 | 36 бит | 9 дней | |
| 2,821 109 9x1012 | 41 бит | 11 месяцев | |
| 1,015 599 5x1014 | 46 бит | 32 года | |
| 3,656 158 4x1015 | 52 бита | 1 162 года | |
| 1,316 217 0x1017 | 58 бит | 41 823 года | |
| 4,738 381 3x1018 | 62 бита | 1 505 615 лет |
Таким образом, пароли длиной до 7 символов включительно в общем случае не являются надежными.
 2018-01-08
2018-01-08 794
794








