Системи диференціальних рівнянь

Нехай необхідно знайти розв’язок задачі Коші для системи звичайних диференціальних рівнянь першого порядку, які записані у стандартній формі

, ,

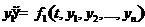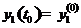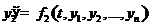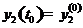, , (6.25)

………………………………………

, .

Якщо ввести векторні позначення

, , , ,

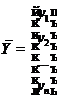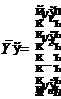то задачу Коші (6.25) можна записати у такому компактному вигляді:

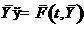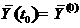, . (6.26)

Векторне рівняння (6.26) за своєю структурою аналогічне скалярному рівнянню (6.1). Це означає, що для задачі (6.26), яка подана у вигляді векторного рівняння, у принципі, можна застосувати будь-який числовий метод розв’язку звичайних диференціальних рівнянь, який розглядався раніше. При цьому скалярним величинам у формулах, які визначені відповідними методами, скалярними величинами є тільки змінна та розрахунковий крок 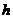; всім іншим величинам відповідають вектори розмірності . Необхідно лише врахувати, що при контролі за точністю розв’язку замість умови (6.21) потрібно використовувати аналогічну умову, в якій замість модуля треба взяти норму відповідного вектора, наприклад, норму-максимум.

Для вектора 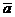з компонентами 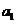, , 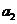…, норма-вектор буде такою:

. (6.27)

Контрольні питання та завдання

1 Які недоліки притаманні методу Ейлера розв'язку диференціальних рівнянь?

2 Який порядок похибки методу Ейлера?

3 Порівняйте між собою методи Ейлера і Гюна.

4 Яка особливість методів сімейства Рунге-Кутта?

5 Який вигляд має загальна ітераційна процедура у методі Рунге-Кутта?

6 Як із загальної процедури Рунге-Кутта отримати метод Хойна і метод середньої точки?

7 Який порядок точності розв'язку диференціальних рівнянь забезпечує метод Рунге-Кутта?

8 Яка відмінність методу Кутта-Мерсона від методу Рунге-Кутта?

9 Яка особливість розв'язку систем диференціальних рівнянь у порівняння з розв'язками скалярних диференціальних рівнянь?