Часть 2. «магнетизм. Оптика. Теоретическая механика. Основы атомной и ядерной физики»

 

1. По двум длинным параллельным проводам текут в одинаковом направлении токи силой I₁ = 10 A и I₂ = 15 А. Расстояние между проводами а = 10 см. Определить напряженность магнитного в точке, удаленной от первого провода на r₁ = 8 см и от второго на r₂ = 6 см.

2. Протон влетел в магнитное поле перпендикулярно линиям индукции и описал дугу радиусом R = 10 см. Определить скорость протона, если магнитная индукция В = 1 Тл.

3. Электрон в однородном магнитном поле движется по винтовой линии радиусом R = 5 см и шагом h = 20 см. Определить скорость электрона, если магнитная индукция В = 0,1 мТл.

4. По двум параллельным проводам длиной l = 3 м каждый текут одинаковые токи силой I = 500 А. Расстояние между проводниками d = 10 см. Определить силу взаимодействия проводников.

5. В соленоид длиной l = 0,1 м, имеющий 300 витков, введен магнитный сердечник. По соленоиду проходит ток I = 1 A. Найти вектор намагничивания железа внутри соленоида.

6. Точка совершает гармонические колебания, уравнение которых имеет вид x = Asinwt, где А = 5 см; w = 2 с^-1. Найти момент времени (ближайший к началу отсчета), в который потенциальная энергия точки П = 10^-4 Дж, а возвращающая сила F = 5×10^-3 Н. Определить также фазу колебаний в этот момент времени.

7. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых x₁ = A₁sinw₁t и y₂ = A₁cosw₂t, где A₁ = 8 см; A₂ = 4 см; w₁ = w₂ = 2 с^-1. Написать уравнение траектории и построить ее. Показать направление движение точки.

8. Плоскополяризованный монохроматический пучок света падает на поляроид и полностью им гасится. Когда на пути пучка поместили кварцевую пластину, интенсивность I пучка света после поляроида стала равной половине интенсивности пучка, падающего на поляроид. Определить минимальную толщину кварцевой пластинки. Поглощением и отражением света поляроидом пренебречь. Постоянную вращения a кварца принять равной 48,9 град/мм.

9. Два николя N₁ и N₂ расположены так, что угол между их плоскостями пропускания составляет a = 60^о. Определить, во сколько раз уменьшается интенсивность I₀ естественного света: 1) при прохождении через один николь N₁; 2) при прохождении через оба николя. Коэффициент поглощения света в николе k =0,05. Потери на отражения света не учитывать.

10. Пучок естественного света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины пучок света образует угол j = 97^о с падающим пучком. Определить показатель преломления n₁ жидкости, если отраженный свет максимально поляризован.

11. На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки d = 2 мкм. Определить наибольший порядок дифракционного максимума, который дает эта решетка в случае красного (l₁ = 0,7 мкм) и в случае фиолетового l₂ = 0,41 мкм) света.

12. От двух когерентных источников S₁ и S₂ (l = 0,8 мкм) лучи попадают на экран. На экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили мыльную пленку (n = 1,33), интерференционная картина изменилась на противоположную. При какой наименьшей толщине d_min пленки это возможно?

13. На дне сосуда наполненного до высоты h водой, находится точечный источник света. На поверхности воды плавает круглый диск так, что его центр находится над источником. При каком минимальном диаметре диска лучи от источника не будут выходить из воды?

14. При прохождении света через трубку длиной l ₁ = 20 см, содержащую раствор сахара концентрацией C₁ = 10%, плоскость поляризации света повернулась на угол j₁ = 13,3^о. В другом растворе сахара, налитом в трубку длиной l ₂ = 15 см, плоскость поляризации повернулась на угол j₂ = 5,2^о. Определить концентрацию C₂ второго раствора.

15. На щель шириной а = 20 мкм падает нормально параллельный пучок монохроматического света (l = 500 нм). Найти ширину А изображения щели на экране, удаленном от щели на расстоянии l = 1 м. Шириной изображения считать расстояние между первыми дифракционными минимумами, расположенными по обе стороны от главного максимума освещенности.

16. Какую энергетическую светимость имеет абсолютно черное тело, если максимум спектральной плотности его энергетической светимости приходится на длину волны λ = 484 нм.

28. Определить радиус a₀ первой боровской орбиты и скорость электрона v на ней. Какова напряженность поля ядра на первой орбите.

29. α – частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину l ящика, если минимальная энергия α - частицы 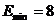MэВ.

30. Во сколько раз изменится период Т вращения электрона в атоме водорода, если при переходе в невозбужденное состояние атом излучил фотон с длиной волны λ=97,5 нм?

31. Определить длину волны, соответствующую границе серии Бальмера.

32. Частица находится в одномерной прямоугольной «потенциальной яме» шириной l с бесконечно высокими «стенками». Найти решение уравнения Шредингера в пределах «ямы» (0 ≤ x ≤ l).

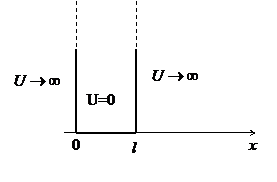33. Определите собственное значение полной энергии гармонического осциллятора, волновая функция которого задана уравнением , где .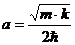

34. Радиальная часть волновой функции для электрона в состоянии 3d имеет вид R(r) = a₃r²e^-r/(3r1). Вычислить расстояние, на котором радиальная составляющая вероятности местонахождения имеет максимум в этом случае.

35. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона.

36. Определите скорость v электрона на третьей орбите водорода (Z=1, n=3).

37. Вычислить дефект массы и энергию связи ядра

38. Найти период полураспада Т_1/2 радиоактивного изотопа, если его активность за время t = 10 суток уменьшилась на 24% по сравнению с первоначальной.

39. В ядерной реакции 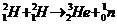выделяется энергия ΔЕ=3,27 МэВ. Определите массу атома , если масса атома 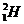равна 3,34461 10^{-27 кг.}