Условия равновесия произвольной пространственной системы сил

БИЛЕТ – 1

«ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ СТАТИКИ»

СТАТИКА – раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел, находящихся под действием сил. РАВНОВЕСИЕ – состояние покоя тела по отношению к другим телам, например по отношению к Земле. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО – тело, расстояние между каждыми двумя точками которого всегда остаётся постоянным. СИЛА – величина, являющаяся основной мерой механического взаимодействия материальных тел. СКАЛЯРНАЯ ВЕЛИЧИНА – величина, которая полностью характеризуется числовым значением величины. ВЕКТОРНАЯ ВЕЛИЧИНА – величина, которая помимо числового значения характеризуется еще и направлением в пространстве. ЛИНИЯ ДЕЙСТВИЯ СИЛ – прямая, вдоль которой направлена сила. СИСТЕМА СИЛ – совокупность сил, действующих на рассматриваемое тело (или тела). ПЛОСКАЯ СИСТЕМА СИЛ – если линия действия всех сил лежит в одной плоскости. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ – если линии действия всех сил не лежат в одной плоскости. СХОДЯЩАЯСЯ СИСТЕМА СИЛ – силы, линии действия которых пересекаются в одной точке. ПАРАЛЛЕЛЬНАЯ СИСТЕМА СИЛ – силы, линии действия которых параллельны друг другу. СВОБОДНОЕ ТЕЛО – тело, которому из данного положения можно сообщить любое перемещение в пространстве. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СИЛ – если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояние покоя или движения, в котором находится тело. УРАВНОВЕШЕННАЯ (ЭКВИВАЛЕНТНАЯ НУЛЮ) СИСТЕМА СИЛ – система сил, под действием которой свободное твердое тело может находиться в покое. РАВНОДЕЙСТВУЮЩАЯ СИСТЕМА СИЛ – если данная система сил эквивалентна одной силе. УРАВНОВЕШИВАЮЩАЯ СИЛА – сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой. ВНЕШНИЕ СИЛЫ – силы, которые действуют на данное тело (или на тела системы) со стороны других тел. ВНУТРЕННИЕ СИЛЫ – силы, с которыми части данного тела (или тела данной системы) действуют друг на друга. СОСРЕДОТОЧЕННАЯ СИЛА – сила, приложенная к телу в какой-нибудь одной его точке. РАСПРЕДЕЛЕННЫЕ СИЛЫ – силы, действующие на все точки данного объёма или данной части поверхности тела. ЦЕНТР ТЯЖЕСТИ ТЕЛА – линия действия равнодействующей сил тяжести проходит через точку.

БИЛЕТ – 2

«АКСИОМЫ СТАТИКИ».

АКСИОМА – 1: Если на свободное абсолютное твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F₁=F₂) и направлены вдоль одной прямой в противоположные стороны. АКСИОМА – 2: Действие данной системы сил на абсолютно твердое тело не изменяется, если к ней прибавить или от нее отнять уравновешенную систему сил. СЛЕДСТВИЕ: Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль её линии действия в любую другую точку тела. ЗАКОН ПАРАЛЕЛЛОГРАММА СИЛ: Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах. ЗАКОН РАВЕНСТВА ДЕЙСТВИЯ И ПРОТИВОДЕЙСТВИЯ: При всяком действии одного материального тела на другое имеет место такое же численно, но противоположное по направлению противодействие. ПРИНЦИП ОТВЕРДЕВАНИЯ: Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым).

БИЛЕТ – 3

«ОСНОВНЫЕ ВИДЫ СВЯЗЕЙ И ИХ РЕАКЦИИ».

СВЯЗЬ – все то, что ограничивает перемещения данного тела в пространстве. СИЛА ДАВЛЕНИЯ НА СВЯЗЬ – тело, стремясь под действием приложенных сил осуществить перемещение, которому препятствует связь, будет действовать на неё с некоторой силой, называемой силой давления на связь. СИЛА РАЕКЦИИ(ПРОТИВОДЕЙСТВИЯ) СВЯЗИ ИЛИ РЕАКЦИЯ СВЯЗИ – сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям.

РЕКЦИИ СВЯЗЕЙ:

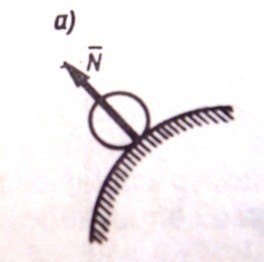1)ГЛАДКАЯ ПЛОСКОСТЬ(ПОВЕРХНОСТЬ) ИЛИ ОПОРА. ГЛАДКАЯ ПОВЕРХНОСТЬ – поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпендикуляра(нормали) к поверхностям соприкасающихся тел в точке их касания. Поэтому реакция 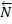гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке.

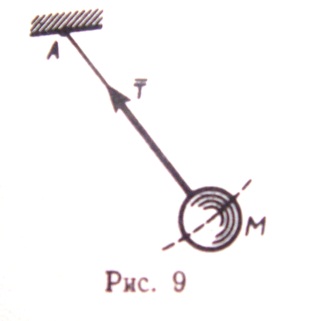
2)НИТЬ. Связь, осуществленная в виде гибкой нерастяжимой нити, не дает телу М удаляться от точки подвеса нити по направлению АМ. Поэтому реакция 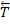натянутой нити направлена вдоль нити к точке её подвеса.

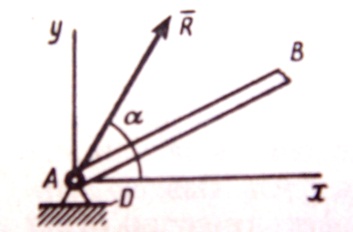3)ЦИЛИНДРИЧЕСКИЙ ШАРНИР (ПОДШИПНИК) - осуществляет такое соединение двух тел, при котором одно тело может вращаться по отношению к другому вокруг общей оси, называемой ОСЬЮ ШАРНИРА. Если тело АВ прикреплено с помощью такого шарнира к неподвижной опоре Д, то точка А тела не может при этом переместиться ни по какому направлению, перпендикулярному оси шарнира. Следовательно, реакция 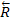цилиндрического шарнира может иметь любое направление в плоскости, перпендикулярной оси шарнира.

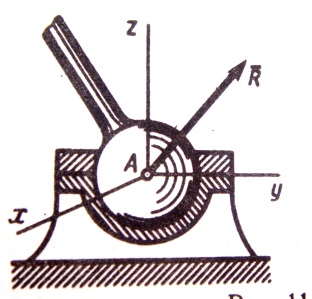4) СФЕРИЧЕСКИЙ ШАРНИР И ПОДПЯТНИК – тела, соединенные сферически шарниром, могут как угодно поворачиваться одно относительно другого вокруг центра шарнира. Примером служит прикрепление фотоаппарата к штативу с помощью шаровой пяты. Если тело прикреплено с помощью такого шарнира к неподвижной опоре, то точка А тела, совпадающая с центром шарнира, не может при этом совершить никакого перемещения в пространстве. Следовательно, реакция 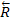сферического шарнира может иметь любое направление в пространстве.

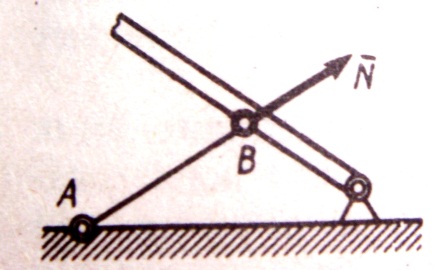5) НЕВЕСОМЫЙ СТЕРЖЕНЬ - стержень, весом которого по сравнению с воспринимаемой им нагрузкой можно пренебречь. Пусть для какого-нибудь находящегося в равновесии тела(конструкции) такой стержень, прикрепленный в точках А и В шарнирами, является связью. Тогда на стержень будут действовать только две силы, приложенные в точках А и В. При равновесии эти силы должны быть направлены вдоль одной прямой, т.е. вдоль АВ. Следовательно, реакция 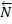невесомого шарнирно прикрепленного прямолинейного стержня направлена вдоль оси стержня.

БИЛЕТ – 4

«СЛОЖЕНИЕ СХОДЯЩИХСЯ СИЛ. СИЛОВОЙ МНОГОУГОЛЬНИК. УСЛОВИЯ РАВНОВЕСИЯ СХОДЯЩИХСЯ СИЛ».

ГЛАВНЫЙ ВЕКТОР – величина, равная геометрической сумме сил какой-нибудь системы.

СЛОЖЕНИЕ СХОДЯЩИХСЯ СИЛ:

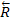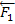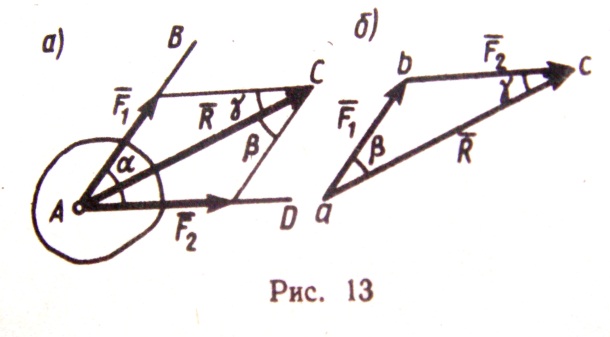
1)СЛОЖЕНИЕ ДВУХ СИЛ – Геометрическая сумма двух сил и 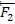находится по правилу параллелограмма или построением силового треугольника, изображающего одну из половин этого параллелограмма. Если угол между силами равен α, то модуль R и углы β, 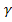, которые сила 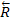образует со слагаемыми силами, определяются по формулам:

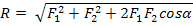(1)

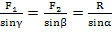(2)

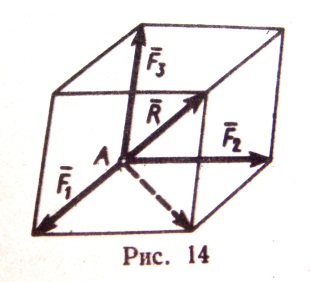
2)СЛОЖЕНИЕ ТРЕХ СИЛ, НЕ ЛЕЖАЩИХ В ОДНОЙ ПЛОСКОСТИ. Геометрическая сумма 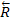трех сил 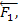s w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 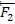, s w:val="24"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 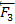, не лежащих в одной плоскости, изображается диагональю параллелипипида, построенного на этих силах (правило параллелипипида).

3) СЛОЖЕНИЕ СИСТЕМЫ СИЛ. Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил 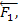s w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 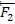, s w:val="24"/></w:rPr><m:t>3</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 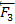…, , 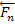откладываем от произвольной точки О вектор 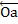, изображающий в выбранном масштабе силу 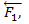от точки а – вектор 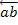, изображающий силу 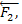от точки b – вектор 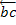, изображающий силу 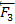и т.д.; от конца m предпоследнего вектора откладываем вектор 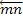, изображающий силу 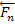. Соединяя начало первого вектора с концом последнего, получаем вектор 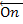= 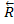, изображающий геометрическую сумму или главный вектор слагаемых сил:

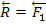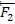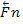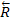+s w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> +…+ или = Ʃ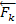

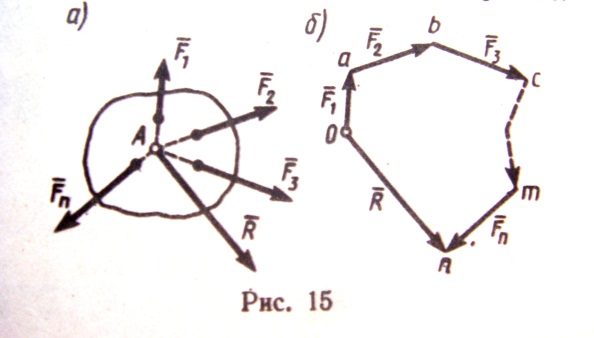
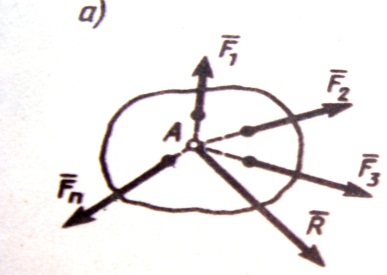4)РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ. Рассмотрим систему сходящихся сил, т.е. сил, линии действия которых пересекаются в одной точке. Т.к. сила, действующая на абсолютно твердое тело, является вектором скользящим, то система сходящихся сил эквивалентна системе сил, приложенных в одной точке. Последовательно применяя закон параллелограмма сил, придем к выводу, что система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке пересечения их линий действия. Следовательно, система сил 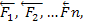изображенных на рисунке 15 а, имеет равнодействующую, равную их главному вектору 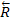и приложенную в точке А(или в любой другой точке, лежащей на линии действия силы 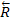, проведенной через точку А.

УСЛОВИЯ РАВНОВЕСИЯ СХОДЯЩИХСЯ СИЛ:

1) ГЕОМЕТРИЧЕСКОЕ УСЛОВИЕ РАВНОВЕСИЯ – Т.к. главный вектор 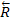системы сил определяется как замыкающая сторона силового многоугольника, построенного из этих сил (рис.15), то 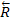может обратиться в нуль только тогда, когда конец последней силы в многоугольнике совпадает с началом первой силы, т.е. когда многоугольник замкнется. Следовательно, для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым. 2)АНАЛИТИЧЕСКИЕ УСЛОВИЯ РАВНОВЕСИЯ – аналитически модуль главного вектора системы сил определяется формулой:

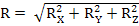Т.к. под корнем стоит сумма положительных слагаемых, то 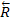обратиться в нуль только тогда, когда одновременно R_X = 0, R_Y = 0, R_Z = 0 т.е., когда действующие на тело силы будут удовлетворять равенствам:

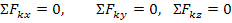
Следовательно, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.

БИЛЕТ – 5

«ТЕОРЕМА О ТРЕХ СИЛАХ».

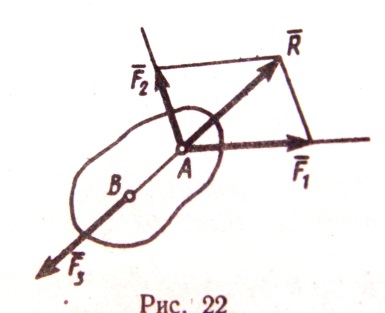
3)ТЕОРЕМА О ТРЕХ СИЛАХ – Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

Для доказательства теоремы рассмотрим сначала какие-нибудь две из действующих на тело сил, например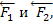

Т.к. по условиям теоремы эти силы лежат в одной плоскости и не параллельны, то их линии действия пересекаются в некоторой точке А. (РИС. 22) Приложим силы 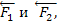в этой точке и заменим их равнодействующей 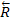. Тогда, на тело будут действовать две силы: сила 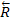и сила 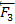приложенная в какой-то точке В тела. Если тело при этом находиться в равновесии, то силы 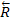и 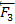должны быть направлены по одной прямой, т.е. вдоль АВ. Следовательно, линия действия силы 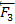тоже проходит через точку А, что и требовалось доказать.

БИЛЕТ – 6

«МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ».

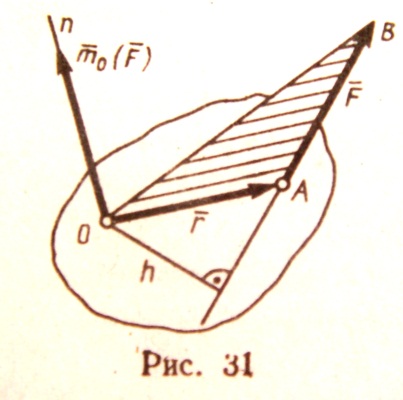
Точку, относительно которой берется момент, называют ЦЕНТРОМ МОМЕНТА, а момент силы относительно этой точки – МОМЕНТОМ ОТНОСИТЕЛЬНО ЦЕНТРА. МОМЕНТОМ СИЛЫ 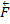ОТНОСИТЕЛЬНО ЦЕНТРА О – называется приложенный в центре О вектор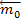 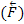, модуль которого равен произведению модуля F силы на её плечо h и который направлен перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки (рис. 31).

Билет-7

«Аналитические выражения момента силы относительно координатных осей»

Возьмем три взаимно перпендикулярные координаты оси x, y, z, которым соответствуют орты I, j, k.

Момент М₀ силы Р относительно начала координат, выражается формулой

М₀=r × P

Где r-радиус-вектор точки А приложения силы относительно начала координат.

Разложим вектор М₀ на составляющие по осям координат:

М₀₌i×M_x+j×M_y+k×M_z

Из векторной алгебры известно, что векторное произведение r×P можно представить определителем:

i j k

r×P= x y z

X Y Z

Приравнивая значения М₀и определителя, разложенного по элементам первой строки, получаем

i×M_x+j×M_y+k×M_z=i×(y×Z-z×Y)+j×(z×X-x×Z)+k×(x×Y-y×X)

Сопоставляя левые и правые части этого равенства, находим проекции момента М₀ на оси координат, равные моментам силы Р относительно этих осей

M_x=y×Z-z×Y; M_y=z×X-x×Z; M_z=x×Y-y×X.

Билет-8

«Сложение параллельных сил. Пара сил. Момент пары.»

Сложение параллельных сил параллельные направленные в одну сторону силы 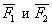приложенные в точках А и В.

Согласно 1-й и 2-й аксиомам статики перейдем от данной системы параллельных сил к эквивалентной системе сходящихся сил 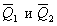. Для этого приложим в точка А и В две уравновешивающие силы 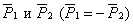направленные вдоль прямой АВ и сложим их с силами 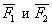по правилу параллелограмма. Полученные силы 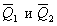перенесем в точку О, где пересекаются их линии действия и разложим на первоначальные составляющие. Силы 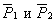отбросим (по 2-й аксиоме статики) и останутся две направленные по одной прямой силы 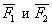. Эти силы переносим в точку С и заменяем равнодействующей 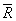модуль которой равен:

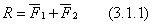
Для определения положения точки С рассмотрим треугольники ОаК, ОАС, ОСВ, Оbm. Из подобия

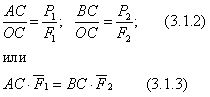
т.к. 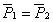. Далее учитывая свойства пропорций, уравнение (3.1.1) и то, что

BC+AC=AB

получаем

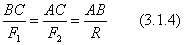
Рассмотрим случай сложения параллельных сдал направленных в разные стороны.

Пусть .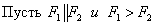

Выберем на продолжении прямой АВ точку С и приложим к ней уравновешенные силы 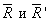которые параллельны 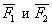. Положение точки С и модули сил выберем таким образом, чтобы удовлетворялись соотношения

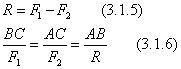
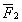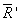Складываем силы и , согласно (3.1.1) и (3.1.4), получим их равнодействующую 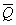равную по модулю 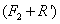, то есть модулю 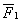и приложенную в точке А. То есть силы 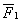и 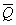оказались уравновешенными и их можно отбросить.

В итоге силы 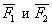заменяются одной силой 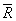, которая и является их равнодействующей. Точка приложения С равнодействующей и ее модуль определяются формулами (3.1.5), (3.1.6).

С помощью формул (3.1.1.) - (3.1.6) можно решать задачу о разложении силы на две ей параллельные. Задача будет определенной при задании дополнительных условий.

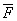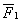Пара сил. Момент пары.Система двух равных по модулю, параллельных и противоположно направленных сил и называется парой сил. Система не находится в равновесии, но и не имеет равнодействующей.

Плоскость, проходящая через линии действия сил называют плоскостью действия пары. Расстояние d между линиями действия сил пары называют плечом пары.

Действие пары сил на твердое тело сводится к вращательному эффекту и зависит от:

1) модуля F и длины плеча d;2) положения плоскости пары;3) направления поворота в этой плоскости.Для характеристики этого вращательного эффекта вводится понятие момент пары.

Моментом пары называется величина, равная взятому с соответствующим знаком произведению модуля одной из сил пары на ее плечо.

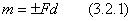Момент пары условимся считать положительным (+), если пара стремится повернуть тело против хода часовой стрелки, и отрицательным (-) - когда по ходу часовой стрелки.

Обозначение момента пары m или М без индекса имеет свой смысл, так как момент пары нельзя смешивать с моментом силы относительно центра и этот центр указывается в индексе (например: 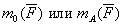). Момент же пары определяется только силами и плечом.

Действие пары сил, как уже указывалось выше, характеризуется тремя условиями. При характеристике пар необходимо задавать все три значения. Но мы знаем, что вектор-нормаль к плоскости задает значения второго и третьего условия. Если мы теперь пронормируем вектор-нормаль значением момента пары, то все три условия будут выполнены. Эти соображения и позволили рассматривать момент пары как вектор. Будем изображать момент пары вектором 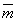или 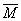, модуль которого равен модулю момента пары, и который направлен перпендикулярно плоскости действия пары, в ту сторону откуда поворот пары виден происходящим против хода часовой стрелки.

Если рассматривать только пары лежащие в одной плоскости, то вместо вектора момента пары, можно стрелкой указывать только направлением поворота.Вектор 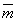на рис. 25 условно изображен выходящим из точек В и D, однако он может изображаться выходящим из середины АВ или CD или из произвольной точки плоскости действия пары, так как

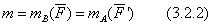
БИЛЕТ – 9

«ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ ПАР».

ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР: Две пары сил, имеющие одинаковые моменты, эквивалентны друг другу. Это следует из того, что указанными операциями, т.е. путем изменения плеча и перемещения пары в плоскости действия или переноса в параллельную плоскость, пары с одинаковыми моментами могут быть преобразованы одна в другую.

БИЛЕТ – 10

«СЛОЖЕНИЕ ПАР»

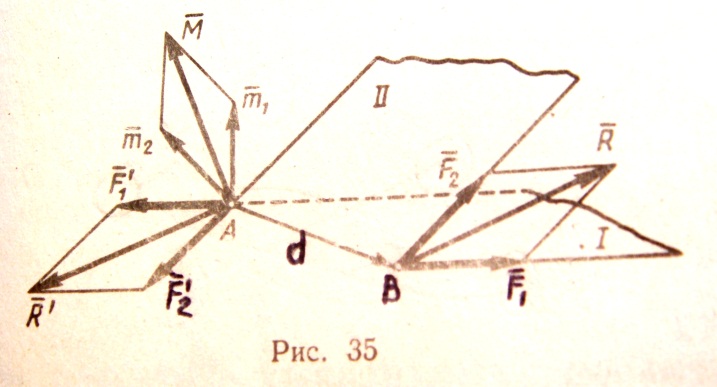
ТЕОРЕМА О СЛОЖЕНИИ ПАР: система пар, действующих на абсолютно твердое тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов слагаемых пар

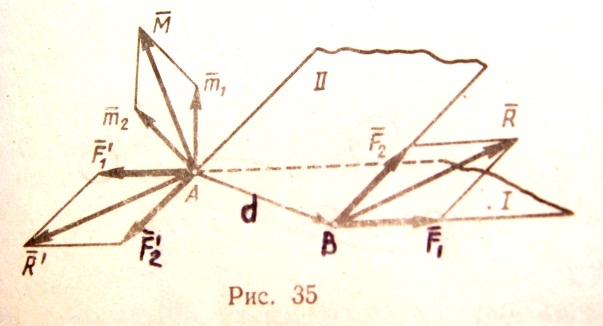
Рассмотрим сначала две пары с моментам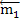и и 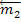, лежащие в плоскостях I и II (рис.35). Возьмем на линии пересечения плоскостей отрезок АВ = d и изобразим пару с моментом 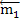силами s w:val="24"/></w:rPr><m:t>1</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 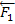и 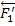, а пару с моментом 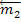- силами s w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 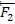и 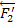. Сложив силы, приложенные в точках А и В, убеждаемся, что пары s w:val="24"/></w:rPr><m:t>1</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 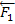и 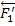s w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 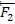и 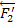действительно эквивалентны одной паре 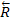, 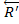. Найдем момент 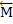этой пары. 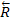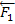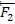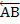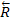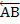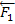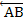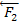Так как = + , то * = * + * или = +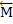

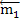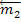
БИЛЕТ-11

Для любой системы сил, приложенных к твёрдому телу, можно найти эквивалентную систему сил, состоящую из силы, приложенной в заданной точке (центре приведения), и пары сил. Эта сила называется главным вектором системы сил, а момент, создаваемый парой сил — главным моментом относительно выбранного центра приведения. Главный вектор равен векторной сумме всех сил системы и не зависит от выбранного центра приведения. Главный момент равен сумме моментов всех сил системы относительно центра приведения.

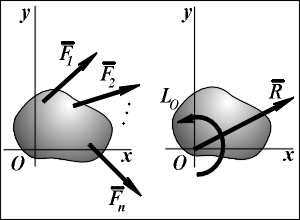Осн теор статики (теорема Пуансо): Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения.

БИЛЕТ-12

Условия равновесия произвольной пространственной системы сил

Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости.

Согласно основной теореме статики (теореме Пуансо) любую произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента системы сил).

Отсюда вытекает условие равновесия произвольной пространственной системы сил.

В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю

R = 0, M_o= 0.

В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю

ΣF_kx = 0, ΣF_ky = 0, ΣF_kz = 0,

M_x(F_k) = 0, M_y(F_k) = 0, M_z(F_k) = 0.

БИЛЕТ-13

Условия равновесия Для равновесия произвольной пространственной системы параллельных сил

Для равновесия пространственной системы параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную силам, и суммы их моментов относительно двух других координатных осей были равны нулю. 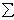F_iz = 0; 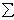M_Ox(F _i) = 0; 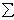M_Oy(F _i) = 0