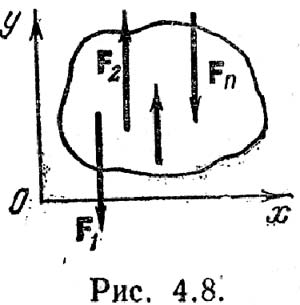
для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на две координатные оси и алгебраическая сумма моментов всех сил относительно произвольной точки равнялись нулю. Второй формой уравнения равновесия является равенство нулю алгебраических сумм моментов всех сил относительно любых трех точек, не лежащих на одной прямой; åMAz(Fk)=0, åMBz(Fk)=0, åMCz(Fk)=0, (5.17), где A, В и С– указанные точки. Необходимость выполнения этих равенств вытекает из условий (5.15). Докажем их достаточность. Предположим, что все равенства (5.17) выполняются. Равенство нулю главного момента при центре приведения в точке А возможно, либо если система приводится к равнодействующей (R≠0) и линия ее действия проходит через точку А, либо R=0; аналогично равенство нулю главного момента относительно точек В и С означает, что либо R≠0 и равнодействующая проходит через обе точки, либо R=0. Но равнодействующая не может проходить через все эти три точки А, В и С (по условию они не лежат на одной прямой). Следовательно, равенства (5.17) возможны лишь при R=0, т. е. система сил находится в равновесии. Заметим, что если точки А, В и С лежат на одной прямой, то выполнение условий (5.17) не будет достаточным условием равновесия, — в этом случае система может быть приведена к равнодействующей, линия действия которой проходит через эти точки.
БИЛЕТ-15
Условия равновесия плоской системы сил
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций на оси координат были равны нулю и сумма моментов всех сил относительно центра О была равна нулю.
2. Вторая форма условий равновесия.Для равновесия произвольной плоской системы необходимо и достаточно, чтобы сумма моментов относительно двух произвольно взятых точек тела была равна нулю и сумма проекций сил на одну из осей координат была равна нулю: 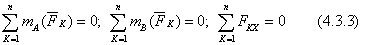
3. Уравнения трех моментов. 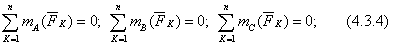 Дополнительное условие: А, В, С не лежат на одной прямой.
Дополнительное условие: А, В, С не лежат на одной прямой.
БИЛЕТ – 16
«ТЕОРЕМА ВАРИНЬОНА»
ТЕОРЕМА ВАРИНЬОНА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ: Если система сил, приложенных к абсолютно твердому телу имеет равнодействующую, то момент равнодействующей относительно произвольного центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси). Векторная записьтеоремы: 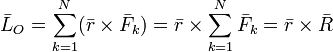 .
.
Билет-17
«Расчет составных конструкций»
План решения задачи на определение реакций опор составной конструкции.1) К конструкции прикладывают все задаваемые силы.2) Согласно принципу освобождаемости тел от связей отбрасывают мысленно внешние связи, заменяя их соответствующими реакциями.3) Установив, что число неизвестных реакций связей превышает число уравнений равновесия, которые можно составить для полученной системы сил, конструкцию расчленяют, заменяя внутренние связи соответствующими реакциями.4) Каждое из тел, входящих в состав конструкции, рассматривают как свободное, находящееся под действием задаваемых сил и реакций внешних и внутренних связей.
5) Сопоставляя общее число неизвестных величин и число всех уравнений равновесия сил, которые могут быть составлены после расчленения конструкции, устанавливают, является ли задача статически определенной6) Составляют уравнения равновесия сил, приложенных к каждому телу.
7) Если задача статически определенна, то полученную систему уравнений решают в наиболее удобной последовательности и определяют все неизвестные величины.
БИЛЕТ – 18
«МЕТОДЫ РАСЧЕТА ПЛОСКОЙ ФЕРМЫ»
ФЕРМА – жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. ПЛОСКАЯ ФЕРМА – если все стержни фермы лежат в одной плоскости. УЗЛЫ – места соединения стержней фермы.
МЕТОДЫ РАСЧЕТА ПЛОСКОЙ ФЕРМЫ: 1) МЕТОД ВЫРЕЗАНИЯ УЗЛОВ – Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов.
2)МЕТОД СЕЧЕНИЙ (МЕТОД РИТТЕРА) – Этим методом удобно пользоваться для определения усилий в отдельных стержнях фермы, в частности для проверочных расчетов. Ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т.е. считая стержни растянутыми. Затем составляют уравнения равновесия, беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.
БИЛЕТ – 19»
«ТРЕНИЯ СКОЛЬЖЕНИЯ. УГОЛ ТРЕНИЯ. КОНУС ТРЕНИЯ».
При стремлении двигать одно тело по поверхности другого в плоскости соприкосновения тел возникает сила сопротивления их относительному скольжению, называемая СИЛОЙ ТРЕНИЯ СКОЛЬЖЕНИЯ. При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения (или сила сцепления), которая может принимать любые значения от нуля до значения FПР, называемого ПРЕДЕЛЬНОЙ СИЛОЙ ТРЕНИЯ.
(FПР = f0N). Равновесие, имеющее место, когда сила трения равна 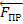 называется ПРЕДЕЛЬНЫМ РАВНОВЕСИЕМ.
называется ПРЕДЕЛЬНЫМ РАВНОВЕСИЕМ.
(F = fN).
УГОЛ ТРЕНИЯ – наибольший угол ϕ0, который полная реакция шероховатой связи образует с нормалью к поверхности. Из чертежа видно, что
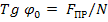
Так как FПР = f0N, то отсюда находим следующую связь между углом трения и коэффициентом трения:
 f0
f0
 При равновесии полная реакция
При равновесии полная реакция 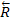 в зависимости от сдвигающих сил может проходить где угодно внутри угла трения. Когда равновесие становится предельным, реакция будет отклонена от нормали на угол
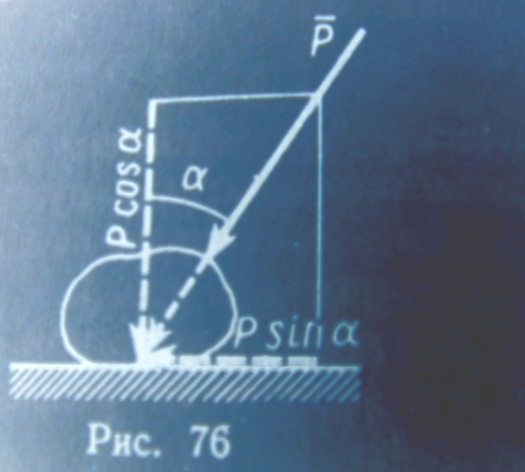
в зависимости от сдвигающих сил может проходить где угодно внутри угла трения. Когда равновесие становится предельным, реакция будет отклонена от нормали на угол 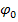 . Если к телу, лежащему на шероховатой поверхности, приложить силу
. Если к телу, лежащему на шероховатой поверхности, приложить силу 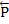 , образующую угол α с нормалью (рис.76), то тело сдвинется только тогда, когда сдвигающее усилие Psinα будет больше
, образующую угол α с нормалью (рис.76), то тело сдвинется только тогда, когда сдвигающее усилие Psinα будет больше 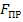 = f0 Pcosα. Но неравенство Psinα > f0 Pcosα, в котором f0 =
= f0 Pcosα. Но неравенство Psinα > f0 Pcosα, в котором f0 = 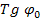 , выполняется только при tgα > tg
, выполняется только при tgα > tg  , т.е. при α>ϕ0 . Следовательно, никакой силой, образующей с нормалью угол α, меньший угла трения
, т.е. при α>ϕ0 . Следовательно, никакой силой, образующей с нормалью угол α, меньший угла трения  , тело вдоль данной поверхности сдвинуть нельзя.
, тело вдоль данной поверхности сдвинуть нельзя.
БИЛЕТ – 20
«ТРЕНИЕ КАЧЕНИЯ»
ТРЕНИЕ КАЧЕНИЯ – сопротивление, возникающее при качении одного тела по поверхности другого.
Рассмотрим круглый цилиндрический каток радиуса R и веса Р, лежащий на горизонтальной шероховатой плоскости. Приложим к оси катка силу 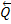 (рис.83 а), меньшую
(рис.83 а), меньшую 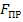 . Тогда в точке А возникает сила трения
. Тогда в точке А возникает сила трения 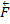 , численно равная Q, которая будет препятствовать скольжению цилиндра по плоскости. Если считать нормальную реакцию
, численно равная Q, которая будет препятствовать скольжению цилиндра по плоскости. Если считать нормальную реакцию 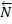 тоже приложенной в точке А, то она уравновесит силу
тоже приложенной в точке А, то она уравновесит силу 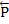 , а силы
, а силы 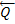 и
и 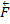 образуют пару, вызывающую качение цилиндра. Фактически следствие деформаций тел касание двух этих цилиндров происходит вдоль некоторой площадки АВ
образуют пару, вызывающую качение цилиндра. Фактически следствие деформаций тел касание двух этих цилиндров происходит вдоль некоторой площадки АВ
(рис. 83 б). При действии силы 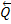 интенсивность давления у края А убывает, а у края В возрастает. В результате реакция
интенсивность давления у края А убывает, а у края В возрастает. В результате реакция 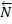 оказывается смещенной в сторону действия силы
оказывается смещенной в сторону действия силы 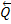 . С увеличением
. С увеличением 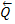 это смещение растет до некоторой предельной величины k. Таким образом, в предельном положении на каток будут действовать пара
это смещение растет до некоторой предельной величины k. Таким образом, в предельном положении на каток будут действовать пара 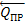 ,
, 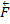 с моментом QПРR и уравновешивающая её пара
с моментом QПРR и уравновешивающая её пара 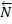 ,
, 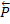 с моментом Nk. Из равенства моментов находим QПРR = Nk или
с моментом Nk. Из равенства моментов находим QПРR = Nk или
QПР =(k/R)N
Пока Q<QПР, каток находится в покое. При Q>QПР начинается качение.
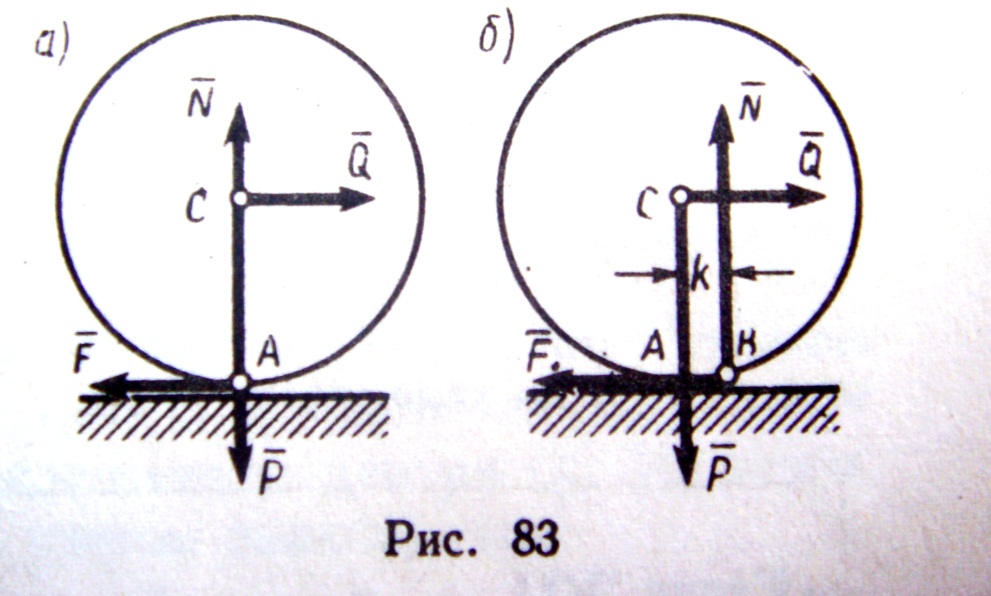
КОЭФФИЦИЕНТ ТРЕНИЯ КАЧЕНИЯ – входящая в формулу (1) линейная величина k. Измеряют величину k обычно в сантиметрах. Значение коэффициента k зависит от материала тел и определяется опытным путем.
Билет-21
«Центр параллельных сил»
Понятие о центре параллельных сил используется при решении некоторых задач механики, в частности при определении положений центров тяжести тел.
Рассмотрим сначала две параллельные силы Р1 и Р2у приложенные к телу в точках А1 и А2 (рис. 103).Очевидно, что эта плоская система сил имеет равнодействующую R=P1+P2, линия действия которой параллельна слагаемым силам и проходит через некоторую точку С, лежащую на прямой A1A2. Положение точки С найдем с
помощью теоремы Вариньона. Согласно этой теореме mc(R) =
=mc(P1)+mc(P2) или 0=P1h1—P2h2=P1*A1C*соs а—Р2*А2С *соs а, откуда
Р1*А1С=Р2-А2С. (54)
В равенство (54) входят модули Р1 и Р2 рассматриваемых сил.
Поэтому, если силы Р1 и Р2 повернуть около точек А1 и А 2 в одну и ту же сторону на один и тот же угол, то образуются две новые параллельные силы Р1 и Р2 имеющие те же модули Р1,Р2; следовательно, для сил Р1, Р2 равенство (54) сохранится и линия действия их равнодействующей R тоже пройдет через точку С. Такая точка называется центром параллельных сил Р1 и Р2.Теперь рассмотрим систему параллельных и одинаково направленных сил Р1, Р2,.. Рп; приложенных к твердому телу в точках -А1, А 2,.. Ап (рис. 104). Эта система сил имеет равнодействующую R=ΣPk
Если каждую из сил системы поворачивать около точки ее приложения в одну и ту же сторону на один и тот же угол, то будут получаться новые системы одинаково направленных параллельных сил с теми же модулями и точками
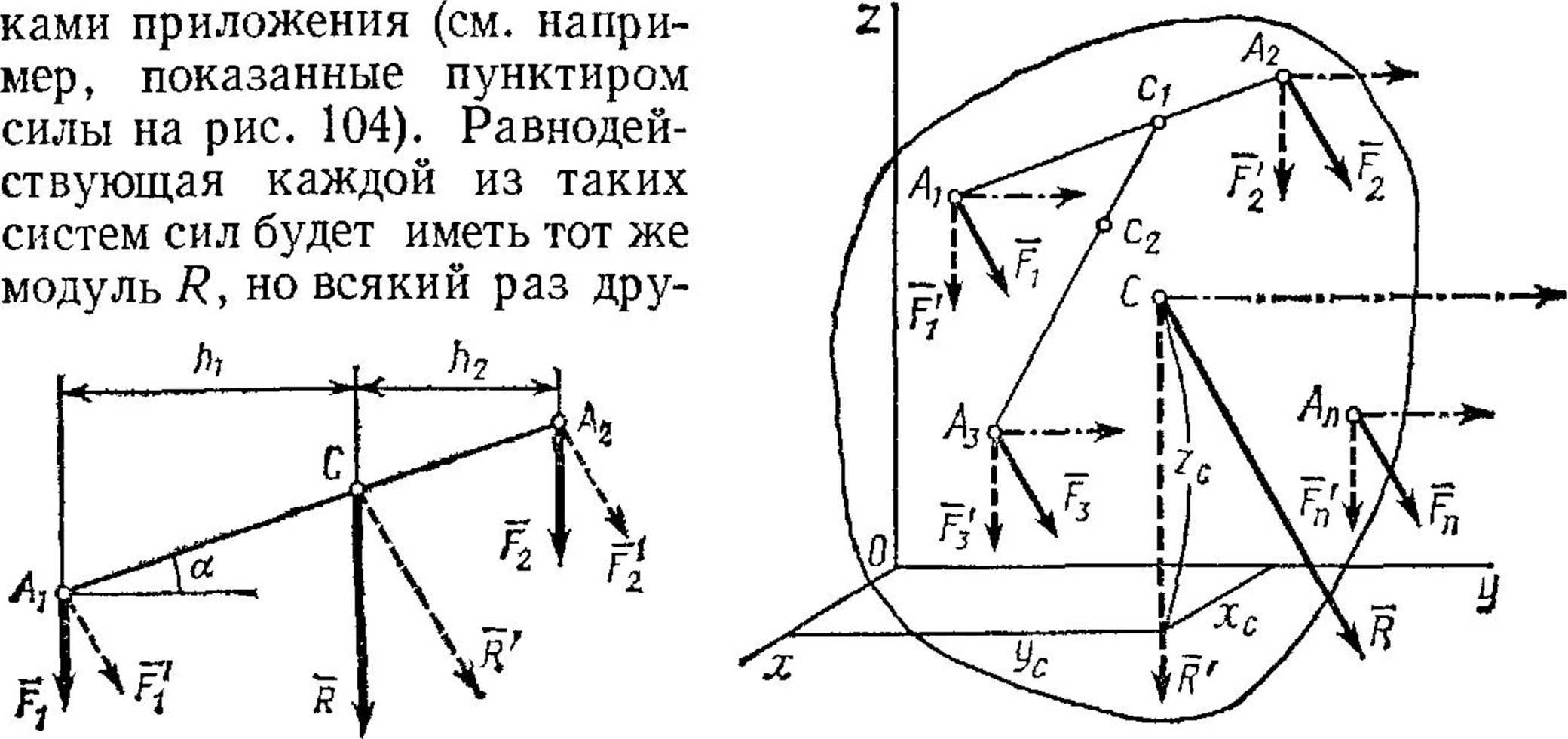
гое направление. Покажем, что при всех таких поворотах линия действия равнодействующей проходит через одну и ту же точку С.В самом деле, сложив сначала силы Р1 и Р2 найдем по формуле (54),что их равнодействующая (на рис. 104 не показана) будет всегда проходить через точку с1 положение которой определяется равенством Р1*А1с1=Р2-А2сг. Сложив затем силы R1 и Р3, найдем, что их равнодействующая, являющаяся одновременно равнодействующей сил Р1,Р2,P3 всегда проходит через аналогично определяемую точку с2, лежащую на прямой с1А3 и т. д. Доведя этот процесс последовательного сложения сил до конца, убедимся, что равнодействующая R всех сил действительно проходит всегда через одну и ту же точку С, положение которой по отношению к точкам А1 А 2,..An т. е. к телу, будет неизменным.Точка С, через которую проходит линия действия равнодействующей системы параллельных сил при любых поворотах этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол, называется центром параллельных сил.
Найдем координаты центра параллельных сил. Положение точки С по отношению к телу является неизменным и от выбора системы координат зависеть не будет. Возьмем поэтому произвольные координатные оси Охуz и обозначим в этих осях координаты точек: А1(х1 y1z1), А(х2, у2, z2),.. С(хс, yс, zс). Пользуясь тем, что от направления сил положение точки С не зависит, повернем сначала силы около их точек приложения так, чтобы они стали параллельны оси Оz, и применим к повернутым силам Р1 Р2.. Рп теорему Варинъона. Так как R является равнодействующей этих сил, то по формуле (46), беря моменты относительно оси Оу, найдем, что my(R)=Σmy(Pk). (56)
Но из чертежа [или из равенств (47)] видно, что mу (R')=Rхс, так как R’=R аналогично mу(Р'1)=Р1х1 так как P’1=P1, и т.д.
Подставляя все эти величины в равенство (56), получим RxС = Р1x1+P2x2+Pnxn=ΣPkxk Отсюда определим хc. Для координаты ус аналогичную формулу найдем, беря моменты относительно оси Ох, Чтобы определить zс, повернем опять все силы, сделав их параллельными оси Оу, и применим к этим силам (изображенным пунктиром с точками) теорему Вариньона, беря моменты относительно оси Ох, Это даст:
-Rzc=-P1z1+(-P2z2)+…+(-Pnzn), откуда определим zс
Окончательно получим следующие формулы для координат центра параллельных сил:
xc=1/RΣPkxk, yc=1/RΣPkyk, zc=1/RΣPkzk, Ус = ^ Ц ркУк> 2с = ^ X.р&’ (57>
где R определяется равенством (55). Заметим, что формулы (55) и (57) будут справедливы и для параллельных сил, направленных в разные стороны, если считать Рк величинами алгебраическими (для одного направления со знаком плюс, а для другого — минус) и если при этом R не равно 0.
 БИЛЕТ – 22
БИЛЕТ – 22
«ЦЕНТР ТЯЖЕСТИ. ОБЩИЕ ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ЦЕНТРА ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ».
ЦЕНТР ТЯЖЕСТИ – неизменно связанная с данным телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве.
ЦЕНТРЫ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ:
ЦЕНТРА ТЯЖЕСТИ ДУГИ ОКРУЖНОСТИ – Рассмотрим дугу 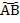 радиуса R с центральным углом АОВ = 2α. В силу симметрии центр тяжести этой дуги лежит на оси ОХ (рис.109).
радиуса R с центральным углом АОВ = 2α. В силу симметрии центр тяжести этой дуги лежит на оси ОХ (рис.109).
Найдем координату ХС по формулам:
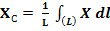
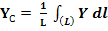
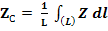 (1)
(1)
Для этого выделим на дуге 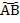 элемент ММ’ длиной d
элемент ММ’ длиной d 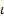 = R dϕ, положение которого определяется углом ϕ. Координата х элемента ММ' будет х = R cosϕ. Подставляя эти значения х и d
= R dϕ, положение которого определяется углом ϕ. Координата х элемента ММ' будет х = R cosϕ. Подставляя эти значения х и d 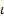 в первую из формулы (1) и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
в первую из формулы (1) и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
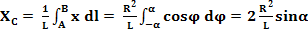 (2)
(2)
Где L – длина дуги 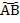 , равная R*2α. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном
, равная R*2α. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О, равном
ХС = (Rsinα)/α (3)
Где угол α измеряется в радианах.
1) 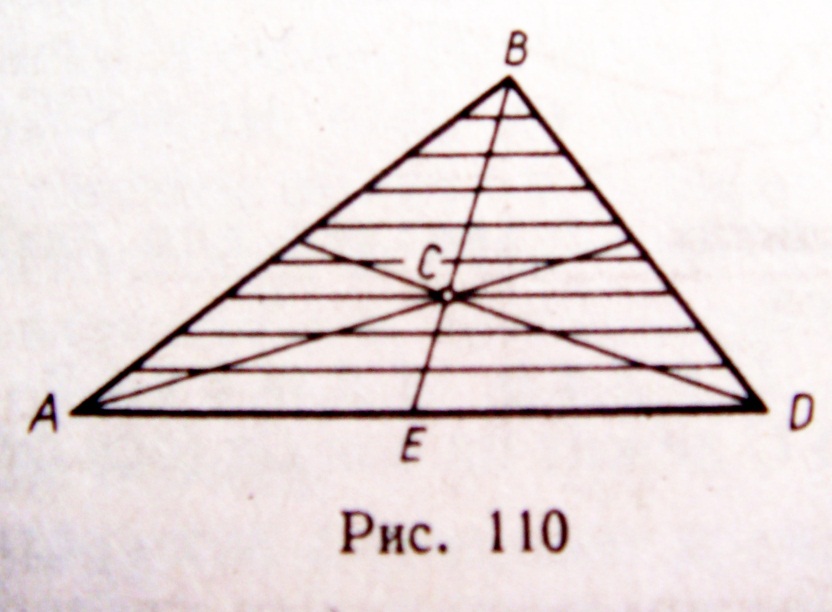 ЦЕНТР ТЯЖЕСТИ ПЛОЩАДИ ТРЕУГОЛЬНИКА – Разобьём площадь треугольника ABD (рис.110)прямыми, параллельными стороне AD, на n узких полосок; центры тяжести этих полосок будут лежать на медиане ВЕ треугольника. Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан. При этом, как известно,
ЦЕНТР ТЯЖЕСТИ ПЛОЩАДИ ТРЕУГОЛЬНИКА – Разобьём площадь треугольника ABD (рис.110)прямыми, параллельными стороне AD, на n узких полосок; центры тяжести этих полосок будут лежать на медиане ВЕ треугольника. Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан. При этом, как известно,
СЕ = ВЕ/3. (4)
2) 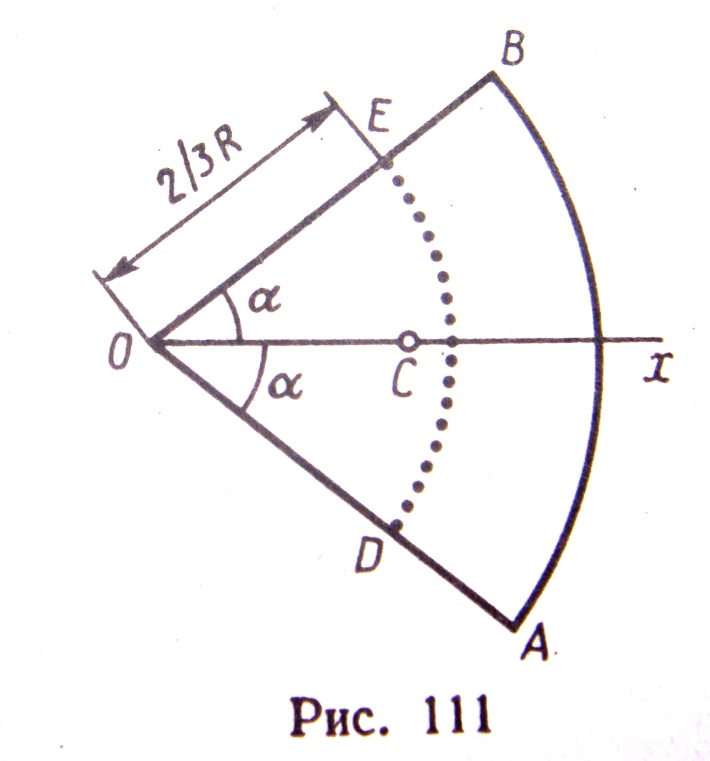 ЦЕНТР ТЯЖЕСТИ ПЛОЩАДИ КРУГОВОГО СЕКТОРА – Рассмотрим круговой сектор OAВ радиуса R с центральным углом 2α (РИС.111). Разобьём мысленно площадь сектора ОАВ радиусами, проведенными из центра О, на n секторов. В пределе, при неограниченном увеличении числа n, эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса 2R/3. Следовательно, центр тяжести секторов ОАВ совпадает с центром тяжести дуги DE, положение которого найдется по формуле (3). Окончательно получим, что центр тяжести площади кругового сектора лежит на его оси симметрии на расстоянии от центра О, равном
ЦЕНТР ТЯЖЕСТИ ПЛОЩАДИ КРУГОВОГО СЕКТОРА – Рассмотрим круговой сектор OAВ радиуса R с центральным углом 2α (РИС.111). Разобьём мысленно площадь сектора ОАВ радиусами, проведенными из центра О, на n секторов. В пределе, при неограниченном увеличении числа n, эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса 2R/3. Следовательно, центр тяжести секторов ОАВ совпадает с центром тяжести дуги DE, положение которого найдется по формуле (3). Окончательно получим, что центр тяжести площади кругового сектора лежит на его оси симметрии на расстоянии от центра О, равном
 (5)
(5)
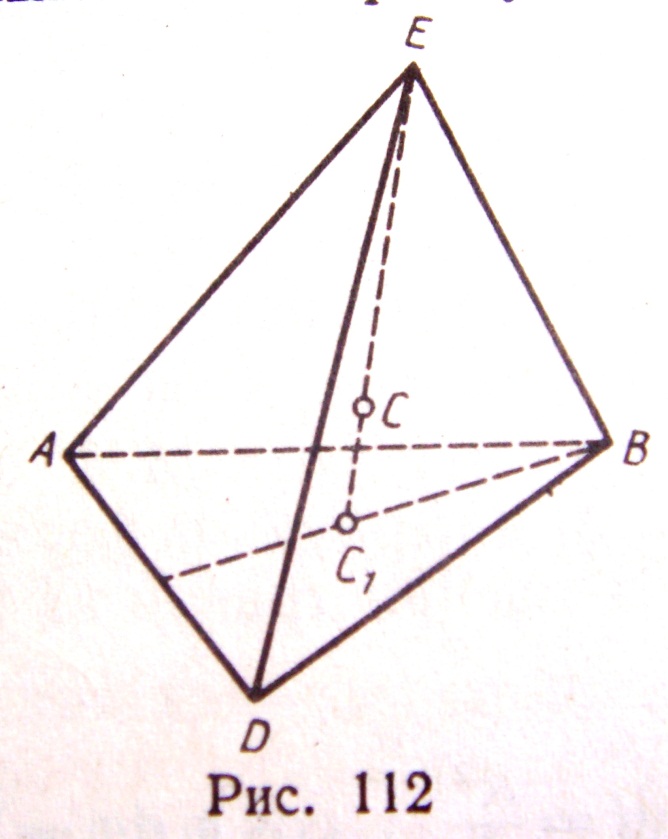
3) ЦЕНТР ТЯЖЕСТИ ОБЪЁМА ПИРАМИДЫ (ИЛИ КОНУСА) – Этот центр С лежит на прямой С1Е (рис.112), где Е – вершина, а С1 – центр тяжести площади основания пирамиды; при этом:
СС1 = ЕС1/4 Результат справедлив для любой многоугольной пирамиды и для конуса.
4) 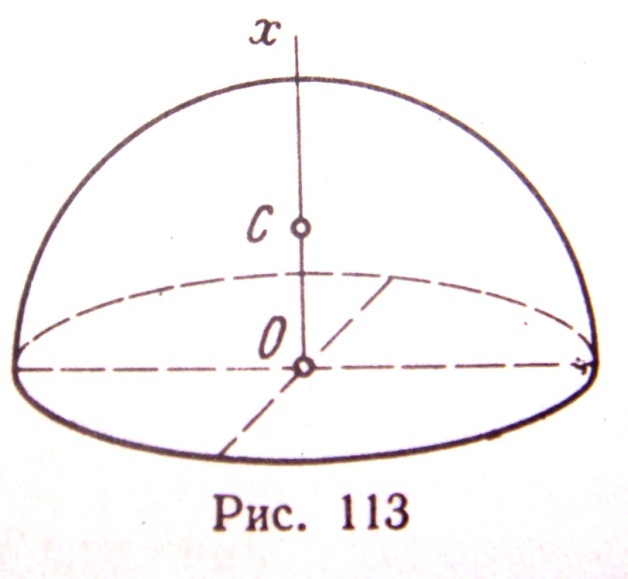 ЦЕНТР ТЯЖЕСТИ ОБЪЁМА ПОЛУШАРА – Этот центр С лежит на оси ОХ (оси симметрии, рис.113), а его координата
ЦЕНТР ТЯЖЕСТИ ОБЪЁМА ПОЛУШАРА – Этот центр С лежит на оси ОХ (оси симметрии, рис.113), а его координата
ХС = ОС =3R/8 (7)
Где R – радиус полушара.
БИЛЕТ – 23
«СПОСОБЫ ОПРЕДЕЛЕНИЯ ЦЕНТРА ТЯЖЕСТИ»
ЦЕНТР ТЯЖЕСТИ – неизменно связанная с данным телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы данного тела, при любом положении тела в пространстве.
СИММЕТРИЯ – Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии. Допустим, например, что однородное тело имеет плоскость симметрии. Тогда этой плоскостью оно разбивается на две такие части, веса которых р1 и р2, равны друг другу, а центры тяжести находятся на одинаковых расстояниях от плоскости симметрии. Следовательно, центр тяжести тела как точка, через которую проходит равнодействующая двух равных и параллельных сил 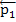 и s w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
и s w:val="24"/></w:rPr><m:t>2</m:t></m:r></m:sub></m:sSub></m:e></m:acc></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 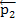 , будет действительно лежать в плоскости симметрии. Из свойств симметрии следует, что центр тяжести, однородного круглого кольца, круглой или прямоугольной пластины, прямоугольного параллелипипида, шара и других однородных тел, имеющих центр симметрии, лежит в геометрическом центре (центре симметрии) этих тел.
, будет действительно лежать в плоскости симметрии. Из свойств симметрии следует, что центр тяжести, однородного круглого кольца, круглой или прямоугольной пластины, прямоугольного параллелипипида, шара и других однородных тел, имеющих центр симметрии, лежит в геометрическом центре (центре симметрии) этих тел.
РАЗБИЕНИЕ – Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести всего тела можно непосредственно вычислить по формулам:
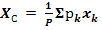
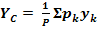 (1)
(1)
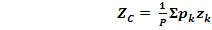
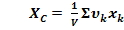
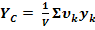 (2)
(2) 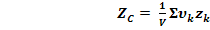
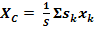
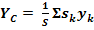 (3)
(3)
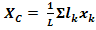
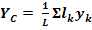 (4)
(4)
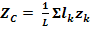
При этом, число слагаемых в каждой из сумм будет равно числу частей, на которые разбито тело.
ДОПОЛНЕНИЕ – Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.
ИНТЕГРИРОВАНИЕ – Если тело нельзя разбить на несколько конечных частей, положения центров тяжести которых известны, то тело разбивают сначала на произвольные малые объёмы 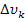 , для которых формулы:
, для которых формулы:
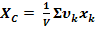
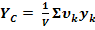 (5)
(5)
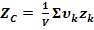
принимают вид:
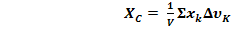 И Т.Д., (6)
И Т.Д., (6)
Где 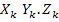 – координаты некоторой точки, лежащей внутри объёма
– координаты некоторой точки, лежащей внутри объёма 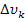 . Затем в равенствах
. Затем в равенствах 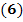 и т.д. переходят к пределу, устремляя все
и т.д. переходят к пределу, устремляя все 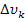 к нулю, т.е. стягивая эти объёмы в точки. Тогда стоящие в равенствах суммы обращаются в интегралы, распространённые на весь объём тела, и формулы (6) дают в пределе:
к нулю, т.е. стягивая эти объёмы в точки. Тогда стоящие в равенствах суммы обращаются в интегралы, распространённые на весь объём тела, и формулы (6) дают в пределе:
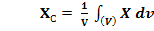
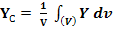 (7)
(7)
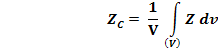
Аналогично для координат центров тяжести площадей и линий получаем в пределе из формул (3) и (4):
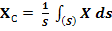
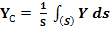 (8)
(8)
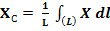
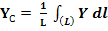
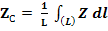 (9)
(9)
1) ЭКСПЕРИМЕНТАЛЬНЫЙ СПОСОБ – Центры тяжести неоднородных тел сложной конфигурации (самолётов, паровозов и т.д.) можно определять экспериментально. Один из возможных экспериментальных методов (метод подвешивания) состоит в том, что тело подвешивают на нити или тросе за различные его точки. Направление нити, на которой подвешено тело, будет каждый раз давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела.
БИЛЕТ-24
Динамический винт
ДИНАМИЧЕСКИЙ ВИНТ - совокупность действующих на твёрдое тело силы 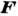 и пары сил с моментом
и пары сил с моментом 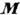 , лежащей в плоскости, перпендикулярной к силе
, лежащей в плоскости, перпендикулярной к силе 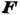 (векторы
(векторы 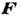 и
и 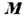 параллельны). К Д. в. приводится в наиб. общем случае произвольная система действующих на твёрдое тело сил. Дальнейшее упрощение Д. в. невозможно, т. е. его нельзя заменить только одной силой (равнодействующей) или одной парой сил. Можно лишь, сложив силу
параллельны). К Д. в. приводится в наиб. общем случае произвольная система действующих на твёрдое тело сил. Дальнейшее упрощение Д. в. невозможно, т. е. его нельзя заменить только одной силой (равнодействующей) или одной парой сил. Можно лишь, сложив силу 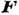 с одной из сил пары, привести Д. в. к двум скрещивающимся силам.
с одной из сил пары, привести Д. в. к двум скрещивающимся силам.
В общем случае для произвольной системы сил главный вектор и главный момент составляют между собой некоторый угол. Главный момент MO разложим на две составляющие, одну из них мы обозначим MO' и направим по главному вектору, а вторую - MO'' - направим перпендикулярно первой (рис. 27, a).
Вторую составляющую представим в виде пары, одной из сил которой уравновесим главный вектор (рис. 27, b). Таким образом, мы привели систему сил к одной силе (по величине и направлению равной главному вектору) и к одной перпендикулярной ей паре с моментом MO', параллельным силе, равным по величине проекции главного момента на главный вектор (рис. 27, c и d). Такую совокупность силы и пары сил называют динамическим винтом, а линию действия AL силы в динамическом винте называют центральной осью системы сил.
БИЛЕТ-25
 2018-01-08
2018-01-08 6493
6493
