Формулировка закона сохранения механической энергии

Полная механическая энергия, т.е. сумма потенциальной и кинетической энергии тела, остается постоянной, если действуют только силы упругости и тяготения и отсутствуют силы трения.

Одномерным называют движение системы с одной степенью свободы. Наиболее общий вид лагранжевой функции такой системы, находящейся в постоянных внешних условиях, есть

L = α(q) 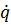² − U (q), (11.1)

где α(q) — некоторая функция обобщенной координаты q. В частности, если q есть декартова координата (назовем ее х), то

L = − U (x). (11.2)

Соответствующие этим лагранжевым функциям уравнения движения интегрируются в общем виде. При этом нет даже необходимости выписывать само уравнение движения, а следует исходить сразу из его первого интеграла — уравнения, выражающего закон сохранения энергии. Так, для функции Лагранжа (11.2) имеем

+ U (x) = Е.

Это есть дифференциальное уравнение первого порядка, интегрирующееся путем разделения переменных. Имеем

= ,

откуда

t = + const. (11.3)

Роль двух произвольных постоянных в решении уравнения движения играют здесь полная энергия Е и постоянная интегрирования const.

Поскольку кинетическая энергия — величина существенно положительная, то при движении полная энергия всегда больше потенциальной, т.е. движение может происходить только в тех областях пространства, где U (х) < Е.

Пусть, например, зависимость U (х) имеет вид, изображенный на рис. 6. Проведя на этом же графике горизонтальную прямую, соответствующую заданному значению полной энергии, мы сразу же выясним возможные области движения. Так в изображенном на рис. 6 случае движение может происходить лишь в области АВ или в области справа от С.

Рис. 6

Точки, в которых потенциальная энергия равна полной

U (х) = Е, (11.4)

определяют границы движения. Они являются точками остановки, поскольку в них скорость обращается в нуль. Если область движения ограничена двумя такими точками, то движение происходит в ограниченной области пространства; оно является, как говорят, финитным. Если же область движения не ограничена или ограничена лишь с одной стороны, — движение инфинитно, частица уходит на бесконечность.

Одномерное финитное движение является колебательным — частица совершает периодически повторяющееся движение между двумя границами (на рис. 6 в потенциальной яме АВ между точками х ₁ и x₂). При этом согласно общему свойству обратимости время движения от х ₁ до x ₂ равно времени обратного движения от x ₂ до x ₁. Поэтому период колебания Т, т.е. время, за которое точка пройдет от x ₁ до x ₂ и обратно, равен удвоенному времени прохождения отрезка x ₁ x ₂ или согласно (11.3)

T (E) = 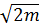, (11.5)

причем пределы х ₁ и x₂ являются корнями уравнения (11.4) при данном значении Е. Эта формула определяет период движения в зависимости от полной энергии частицы.