2018-01-08
826
Для вычисления давления света при нормальном падении излучения и отсутствии рассеяния можно воспользоваться следующей формулой:
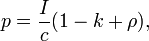
где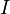 
— количество лучистой энергии, падающей нормально на 1 м² поверхности за 1 с, т. е. интенсивность падающего излучения; 
— скорость света, 
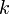— коэффициент пропускания, 
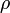— коэффициент отражения.
Давление солнечного света на перпендикулярную свету зеркальную поверхность, находящуюся в космосе в районе Земли, легко рассчитать через плотность потока солнечной (электромагнитной) энергии на расстоянии одной астрономической единицы от Солнца (солнечная постоянная). Оно составляет 4,6 мкН/м² = 4,6·10−11[источник не указан 494 дня] атм (см. солнечная постоянная).
Если свет падает под углом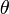 
к нормали, то давление можно выразить формулой:
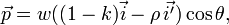
где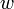 
— объёмная плотность энергии излучения, 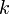— коэффициент пропускания, 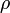— коэффициент отражения, 
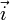— единичный вектор в направлении падающего пучка, 
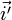— единичный вектор в направлении отражённого пучка.
Например, тангенциальная составляющая силы давления света на единичную площадку будет равна:
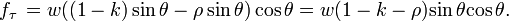
Нормальная составляющая силы давления света на единичную площадку будет равна:
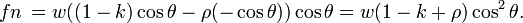
Отношение нормальной и тангенциальной составляющих равно:
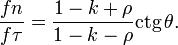
При рассеянии
Если рассеяние света поверхностью и при пропускании, и при отражении подчиняется закону Ламберта, то при нормальном падении давление будет равно: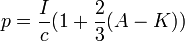 
где 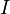— интенсивность падающего излучения, 
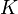— коэффициент диффузного пропускания, 
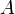— альбедо.
Вывод
Найдём импульс, уносимый электромагнитной волной от Ламбертова источника.
Полная светимость ламбертова источника, как известно, равна:
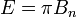
где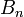 
— сила света в направлении нормали.
Отсюда сила света под произвольным углом 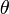к нормали, по закону Ламберта, равна:
. 
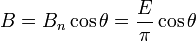
Энергия, излучаемая в элемент телесного угла, имеющий вид сферического кольца, равна:
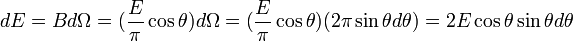
Для определения импульса, уносимого излучением, нужно учитывать только его нормальную составляющую, так как в силу поворотной симметрии все тангенциальные составляющие взаимно компенсируются:
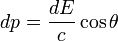
Отсюда
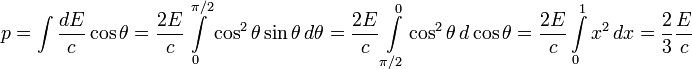
Для рассеянного обратно излучения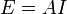 
и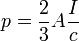 
Для излучения, прошедшего сквозь пластинку,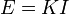 
и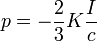 
(минус возникает из-за того, что это излучение направлено вперёд).
Складывая давление, создаваемое падающим и обоими видами рассеянного излучения, получаем искомое выражение.
В случае, когда отражённое и пропущенное излучение является частично направленным и частично рассеянным, справедлива формула:
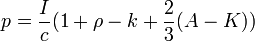
где 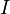— интенсивность падающего излучения, 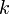— коэффициент направленного пропускания, 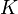— коэффициент диффузного пропускания, 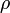— коэффициент направленного отражения, 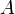— альбедо рассеяния.
