Интегрирование по частям в неопределенном интеграле

Пусть 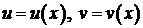– дифференцируемые функции, тогда дифференциал их произведения 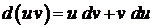. Интегрируя это равенство, получим:

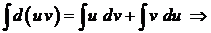
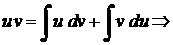
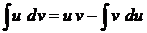- формула интегрирования по частям.

Эта формула применяется к интегрированию выражений, которые можно представить в виде произведения двух сомножителе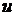й и 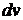так, что отыскание функции 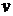по ее дифференциалу 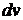и вычисление интеграла 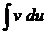составляет в совокупности задачу более простую, чем непосредственное вычисление .

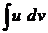Пример. Найти .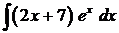

Пусть 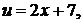тогда все остальное в подынтегральном выражении

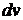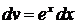: . Найдем 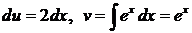. Применяя формулу, получим: .

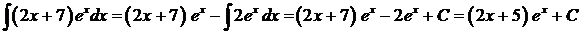Интегрирование рациональных дробей.

Дробью называется выражение вида: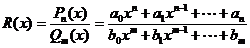

Дробь 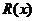- правильная, если 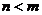. Дробь 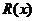- не правильная, если .

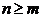Для того, чтобы проинтегрировать дробь надо разложить ее на простейшие дроби.

Простейшие дроби:

1.

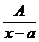
2.

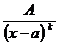
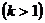
3.

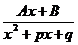
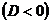
4.

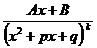
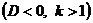
Интеграл от первой дроби - табличный интеграл:

1.

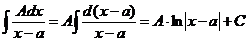
Интеграл от второй дроби - также табличный:

2.

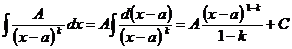
3. Интеграл от третьей дроби см. интеграл группы четырёх.

4. Интеграл от четвертой дроби также см. интеграл группы четырёх.

Рассмотрим теперь дробь более общего вида.

Теорема. Пусть 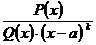- правильная дробь, причем 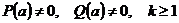. Тогда эту дробь можно представить в виде:

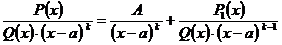
Следствие. Используя эту логику и дальше, можно записать:

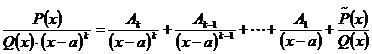
Теорема. Пусть 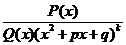- правильная дробь, причем 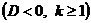. Тогда можно записать: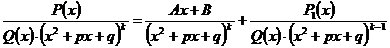

Следствие.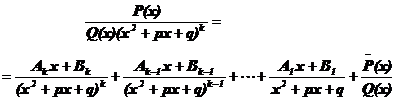

Таким образом, дроби общего вида сводятся к простейшим дробям.