2018-01-08
674
Пусть 
– одна из первообразных 
.
1. 
.
2. 
.
3. 
.
Таблица интегралов:
1. 
| 2. 
|
3. 
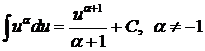
| 4. 
|
5. 
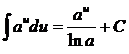
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
11. 
| 12.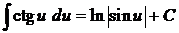 
|
13. 
| 14.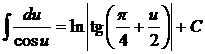 
|
15. 
| 16.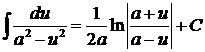 
|
17. 
| 18. 
|
19. 
| 20. 
|
21. 
| 22. 
|
Непосредственное интегрирование.
3. Основныеметоды интегрирования в неопределенном интеграле:
Замена переменной в неопределенном интеграле (или метод подстановки)
Пусть требуется найти неопределенный интеграл 
, но непосредственно подобрать первообразную для не удается, хотя известно, что она существует. Во многих случаях введением вместо переменной интегрирования 
некоторой новой переменной можно данный интеграл свести к другому, который или содержится в таблице основных интегралов или легко вычисляется другим способом.
Такой метод называется методом замены переменной (метод подстановки), или методом подстановки.
Итак, введем новую переменную по формуле 
– дифференцируемая функция на некотором интервале, при этом функция непрерывна на соответствующем интервале изменения . Тогда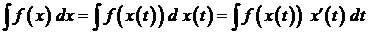 
– формула замены переменной в неопределенном интеграле.
|
|
|
Пример. Найти 
.
Сделаем замену переменной по формуле: 
.
