Задания для выполнения контрольной работы по теме 4.
Задание 1. Вычислить пределы (выбрать один вариант):
| 1 вариант | а) 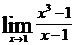
| б) 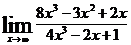
|
| 2 вариант | a) 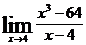
| б) 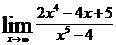
|
| 3 вариант | а) 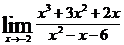
| б) 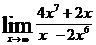
|
| 4 вариант | а) 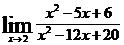
| б) 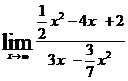
|
| 5 вариант | а) 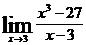
| б) 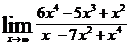
|
| 6 вариант | а) 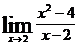
| б) 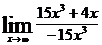
|
| 7 вариант | а) 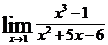
| б) 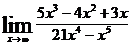
|
| 8 вариант | а) 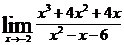
| б) 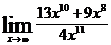
|
| 9 вариант | а) 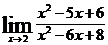
| б) 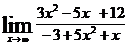
|
| 10 вариант | а) 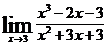
| б) 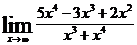
|
Задание 2. Найти производные первого порядка данных функций, используя таблицу производных правила вычисления производных (выбрать один вариант):
1 вариант а) y = 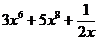 б) y =
б) y = 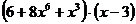
в) y = 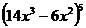 г) y =
г) y = 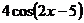 д) y =
д) y = 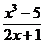
2 вариант а) у = 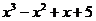 б) у =
б) у = 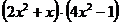
в) у = 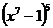 г) у =
г) у = 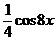 д) у =
д) у = 
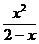
3 вариант а) 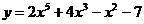 б)
б) 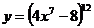
в) 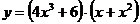 г)
г) 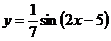 д)
д) 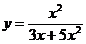
4 вариант а) 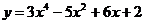 б)
б) 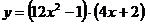
в) 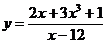 г)
г) 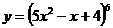 д)
д) 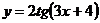
5 вариант а) 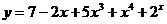 б)
б) 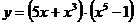
в) 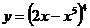 г)
г) 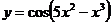 д)
д) 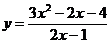
6 вариант а) 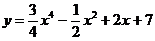 б)
б) 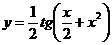
в) 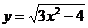 г)
г) 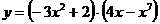 д)
д) 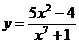
7 вариант а) 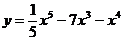 б)
б) 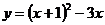
в) 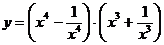 г)
г) 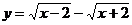 д)
д) 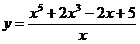
8 вариант а) 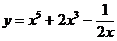 б)
б) 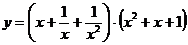
в) 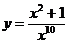 г)
г) 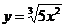 д)
д) 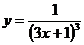
9 вариант а) 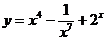 б)
б) 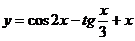
в) 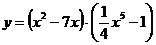 г)
г) 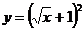 д)
д) 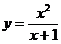
10 вариант а) 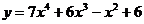 б)
б) 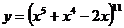
в) 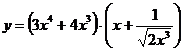 г)
г) 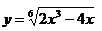 д)
д) 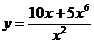
ТЕМА 2: НЕОПРЕДЕЛЁННОЕ ИНТЕГРИРОВАНИЕ. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.
План:
1. Понятие неопределенного интеграла.
2. Свойства неопределенного интеграла. Таблица интегралов. Непосредственное интегрирование.
3. Основные методы интегрирования в неопределенном интеграле: замена переменной в неопределенном интеграле, интегрирование по частям в неопределенном интеграле, интегрирование рациональных дробей.
4. Определенный интеграл и его свойства. Формула Ньютона-Лейбница.
5. Основные методы интегрирования в определенном интеграле: замена переменной в неопределенном интеграле, интегрирование по частям в неопределенном интеграле.
Понятие неопределенного интеграла.
Определение. Функция 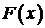 называется первообразной функции
называется первообразной функции  заданной на интервале
заданной на интервале 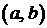 , если она дифференцируема
, если она дифференцируема 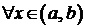 и для любого
и для любого  из этого интервала
из этого интервала 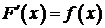 .
.
Определение. Совокупность всех первообразных функции  на интервале
на интервале 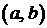 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается
и обозначается  .
.
 называется подынтегральной функцией,
называется подынтегральной функцией, 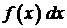 – подынтегральным выражением,
– подынтегральным выражением,  – переменной интегрирования.
– переменной интегрирования.
Свойства неопределенного интеграла. Таблица интегралов. Непосредственное интегрирование.
 2018-01-08
2018-01-08 366
366







