2018-01-08
587
Уравнения, решаемые с использованием определения логарифма
. Данное уравнение равносильно уравнению 
.
Пример 2. Решить уравнение: 
.
Решение. Из определения логарифма следует, что 
, откуда 3х = 6, x =2.
Ответ: 2
Уравнения, решаемые с помощью операции потенцирования
Если 
, то f(x)=g(x). ОДЗ второго уравнения шире, чем первого, следовательно, в результате преобразования могут появиться посторонние корни. Поэтому, решив уравнение f(x)=g(x), следует выполнить проверку, подставляя корни в исходное уравнение, помня при этом, что логарифм отрицательного числа и нуля не существует.
Пример 3. Решить уравнение: 
.
Решение. Потенцируя, получим x 2 - 17 = x + 3,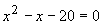 
.
Решив квадратное уравнение, найдем, что 
. Проверка корней показывает, что корень x = -4 является посторонним, поскольку не входит в О.Д.З. переменной x исходного уравнения.
Ответ: 5
Сведение логарифмического уравнения к алгебраическому
Пример 4. Решить уравнение: 
. В ответе указать больший корень уравнения.
Решение. Пусть 
, тогда 
или 
.
Подставляя найденные значения t 1 и t 2 в формулу 
, получим
Оба корня входят в область допустимых значений.
Ответ: 243
Показательное уравнение вида 
.
При решении показательных уравнений данного вида успех часто достигается путем преобразования исходного уравнения в логарифмическое. С этой целью обе части исходного уравнения надо прологарифмировать по одному и тому же основанию.
Пример 5. Решить уравнение: 
. В ответе указать корень уравнения, или, если корней несколько, их сумму.
Решение. Прологарифмировав, получаем 
. Пусть t =lg x, тогда t 2 - t -2 =0 или t 1 = 2, t 2= -1, откуда x 1 = 100, x 2= 0,1. Проверка показывает, что оба корня удовлетворяют исходному уравнению. Находим их сумму.
Ответ: 100,1
