Выполнить минимизацию целевой функции методом дихотомии.
F(x)= 
Решение.
Шаг приращения δ=0.01
Положим a1 = a, b1 = b.


Вычисляем
F( ), F(
), F( )
)
F( )=
)=  -4*
-4*  =1.255025
=1.255025
F( )=
)=  -4*
-4*  =1.245025
=1.245025

Интерация №1.
Поскольку F( ) >F(
) >F( ), то
), то 

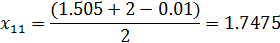

Вычисляем
F(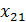 ), F(
), F( )
)
F(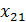 )=
)=  -4*
-4*  =1.0638
=1.0638
F( )=
)= 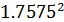 -4*
-4*  =1.0588
=1.0588
Интерация №2.
Поскольку F(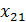 ) >F(
) >F( ), то
), то 



Вычисляем
F( ), F(
), F( )
)
F( )=
)=  -4*
-4*  =1.0159
=1.0159
F( )=
)=  -4*
-4*  =1.0135
=1.0135
Интерация №3.
Поскольку F( ) >F(
) >F( ), то
), то 



Вычисляем
F(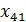 ), F(
), F( )
)
F(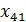 )=
)=  -4*
-4*  =1.004
=1.004
F( )=
)=  -4*
-4*  =1.0028
=1.0028
Интерация №4.
Поскольку F(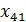 ) >F(
) >F( ), то
), то 



Вычисляем
F( ), F(
), F(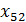 )
)
F( )=
)=  -4*
-4*  =1.004
=1.004
F(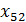 )=
)=  -4*
-4*  =1.0028
=1.0028
Расчёты сведём в таблицу.
| № | 
| 
| 
| 
| 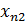
| F( ) )
| F(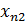 ) )
| 
|
| 1.5 | 1.495 | 1.505 | 1.255 | 1.245 | 0.2525 | |||
| 1.505 | 0.495 | 1.7475 | 1.7575 | 1.0638 | 1.0588 | 0.06563 | ||
| 1.7575 | 0.2425 | 1.8738 | 1.8838 | 1.0159 | 1.0135 | 0.01953 | ||
| 1.8838 | 0.1163 | 1.9369 | 1.9469 | 1.004 | 1.0028 | 0.00832 | ||
| 1.9469 | 0.05313 | 1.9684 | 1.9784 | 1.001 | 1.0005 | 0.00567 |
|1.00337851-1.00070556|≤0.01
Находим x как середину интервала [a,b]:
X= 
Ответ: x=1.9734375; F(x)=1.00070556

ЗАКЛЮЧЕНИЕ
В ходе выполнения курсовой работы были проанализированы численные методы одномерной оптимизации. Математическое описание метода дихотомии. Выполнена минимизация целевой функции методом дихотомии.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
 2018-01-21
2018-01-21 565
565







