2018-01-21
1250
Продольная рабочая арматура в пролёте 4Æ22 A500 с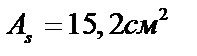 
. Площадь 
определена из расчёта на действие максимального изгибающего момента в середине пролёта. В целях экономии арматуры по мере уменьшения изгибающего момента к опорам два стержня обрываются в пролёте, а два других доводятся до опор. Если продольная рабочая арматура разного диаметра, то до опор доводятся стержни большего диаметра.
Определяем момент, воспринимаемый сечением ригеля с полной запроектированной арматурой 4Æ22 A500 (
).
Из условия равновесия:
, 
,
Рис. 9 Расчетное сечение ригеля в месте обрыва арматуры
Рис. 10 Эпюра материалов
Изгибающий момент, воспринимаемый сечением ригеля, определяем относительно центра тяжести сжатой зоны:
,
M (4Æ22)= 
,
, то есть больше действующего изгибающего момента от полной нагрузки, это значит, что прочность сечения обеспечена.
До опоры доводятся 2Æ22A500 (см. рис. 9), 
, 
,
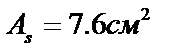
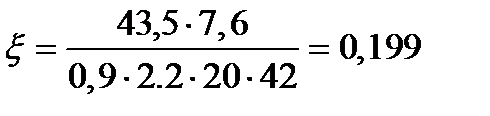Определяем изгибающий момент, воспринимаемый сечением ригеля с рабочей арматурой в виде двух стержней, доводимых до опоры:
M (2Æ22)=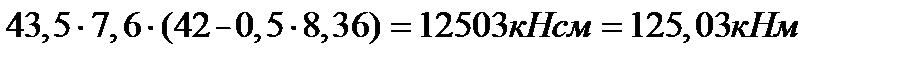 
.
Откладываем в масштабе на эпюре моментов полученные значения изгибающих моментов M (4Æ22) и M (2Æ22) и определяем место теоретического обрыва рабочей арматуры – это точки пересечения эпюры моментов с горизонтальной линией, соответствующей изгибающему моменту, воспринимаемому сечением ригеля с рабочей арматурой в виде двух стержней M (2Æ22) (рис. 10).
Эпюра моментов для этого должна быть построена точно с определением значений изгибающих моментов в 
пролёта.
Изгибающий момент в любом сечении ригеля определяется по формуле:
где 
- опорная реакция, x - текущая координата.
.
При 
,
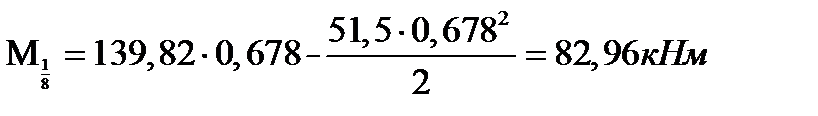
При 
,
При 
.
Длина анкеровки обрываемых стержней определяется по следующей зависимости:
,
Поперечная сила Q определяется графически в месте теоретического обрыва, в данном случае Q =81,62кН. Поперечные стержни Æ8 А400 Rsw =285МПа с Asw =1,01см2 в месте теоретического обрыва имеют шаг 10см
кН/см
< 
см
Место теоретического обрыва арматуры можно определить аналитически. Для этого общее выражение для изгибающего момента нужно приравнять моменту, воспринимаемому сечением ригеля с арматурой 2Æ22 А500 М(2Æ22) =125,03кН·м
; 
; 
м
Это точки теоретического обрыва арматуры.
Длина обрываемого стержня будет равна 4,3-1,13+2×0,33=3,83м. Принимаем длину обрываемого стержня 3,9 м (кратно 5 см).
Определяем аналитически величину поперечной силы в месте теоретического обрыва арматуры x=1,48м.
кН,
Как видно, графически поперечная сила была принята с достаточной степенью точности.
