Использование преобразование Лапласа для исследования динамических систем

В второй половине XIX века английский ученый О. Хевисайд предложил использовать символическое исчисление, в основе которого лежит построение математического анализа как системы формальных операций над символом p = d/dt, где t - независимая переменная. Символическое исчисление оказалось довольно удобным для решения различных прикладных задач, связанных с линейными дифференциальными уравнениями.

Строгое обоснование символического операционного исчисления получило в операционном методе, основанном на преобразовании Лапласа.

Изображением по Лапласу комплексно-значной функции f (t) называют функцию комплексного переменного p = s + iσ, определяемую как

Для преобразования (1) используют символическую запись

f (t) = F (p) или F (p) = f (t).

При этом f (t) называют функцией-оригиналом или просто оригиналом, а F(p) называют изображением.

Предполагается, что оригинал удовлетворяет следующим трем условиям:

1. f (t)=0 для t < 0;

2. f (t) удовлетворяет условию Липшица-Гельдера всюду на оси t > 0 за исключением отдельных точек, где оригинал может иметь разрывы первого рода (при этом считается, что на любом конечном интервале таких точек конечное число);

3. f (t) возрастает не быстрее показательной функции.

С физической точки зрения первое условие оправдано тем, что в роли параметра t обычно выступает время. Дифференциальные же уравнения, описывающие разнообразные физические процессы, решают с заданными начальными условиями. Поэтому можно полагать, что история процесса до момента начала наблюдения определена в начальных условиях. Любая непрерывно-дифференцируемая функция удовлетворяет условию Липшица- Гельдера (2) с α = 1, а условие (3) для физических процессов всегда справедливо.

Основные свойства преобразования Лапласа:

1. Линейность: αf (t) + βg (t) = αF (p) + βG (p)

2. Подобие:

3. Запаздывание

f (t − τ) = e−pτ F (p)

4. Дифференцирование оригинала (смещение)

Дифференцирование оригинала приводит к вычислению изображения по формуле:

f ′ (t) = pF (p) − f (0)

Вычисление производной порядка n позволяет вычислить изображение по формуле:

При f (0) = 0 формула дифференцирование оригинала сводится к умножению изображения на p. Поэтому оператор дифференцирования d/dt действительно можно заменять символом p как в операционном исчислении, но только при оперировании с изображениями по Лапласу.

f ′ (t) = pF (p),

5. Предельные (тауберовы) теоремы

Если f (t) является оригиналом вместе со своей производной f ′ (t), то

lim pF (p) = f (0)

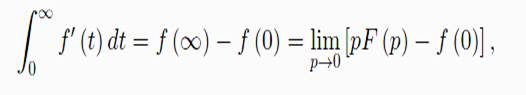p→∞