Раздел 1. Элементарные звенья систем управления

Понятие звена

Звеном системы называется ее элемент (часть), об­ладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь самую разнообразную физическую основу (электриче­ские, гидравлические, механические и т. п.) и конструк­тивное выполнение, но при этом относиться к одной функциональной группе. Соотношение входного и выход­ного сигналов в звеньях одной и той же группы описы­вается одинаковыми дифференциальными уравнениями. Это свидетельствует о том, что такие звенья имеют оди­наковые динамические свойства.

Так как процесс автоматического регулирования оп­ределяется только динамическими свойствами системы (а следовательно, и ее звеньев), то в основу классифи­кации звеньев положены их динамические свойства. Та­кая классификация звеньев по виду описывающих эти звенья дифференциальных уравнений дает возможность разработать стройную теорию АСР и единые методы их исследования и расчета, не зависящие от различий в физических процессах и конструктивных решениях, принятых в основу при проектировании АСР и ее элементов.

Простейшими типовыми звеньями АСР являются: усилительное, интегрирующее, апериодическое, колеба­тельное, дифференцирующее и запаздывающее звенья.

Усилительное звено

В усилительном звене выходная величина в каждый момент времени пропорциональна входной величине, т. е.

x_вых = kx_вх. (1)

[Здесь и в дальнейшем для сокращения записи выраже­ния x_вых(t) и x_вх(t) записываются как x_вых и x_вх. Пере­ходные процессы рассматриваются при нулевых началь­ных условиях.]

 

Коэффициент пропорциональности k называется ко­эффициентом усиления или коэффициентом передачи звена.Уравнение усилительного звена (1) алгебраиче­ское. Это свидетельствует о том, что усилительное зве­но передает сигнал мгновенно, без динамических пере­ходных процессов и искажений.

 

 

 

Рис. 1. Передаточная функция и переход­ный процесс усилительного звена.

 

На рис. 1 представлен характер изменения по вре­мени выходной величины усилительного звена при пода­че на его вход постоянной входной величины x_0вх.

Передаточная функция звена имеет вид:

W(p) = k. (2)

Примерами усилительных звеньев могут служить ме­ханические передачи, потенциометрические датчики, безинерционные усилители (например, электронные) и т. п.

Интегрирующее звено

Выходная величина интегрирующего звена пропор­циональна интегралу входной величины, т. е.

x_вых = k .

Дифференциальное уравнение интегрирующего зве­на имеет вид:

. (3)

Коэффициент k называется коэффициентом усиления или передачи звена по скорости. Он численно равен ско­рости изменения выходной величины при единичном зна­чении входной величины.

Преобразовав дифференциальное уравнение звена (3) по Лапласу, получим:

pX_вых(p) = kX_вх(p),

откуда находим передаточную функцию звена:

W(p) = k/p. (4)

Если входная и выходная величины имеют одинако­вую размерность, то из выражения (3) следует, что коэффициент k имеет размерность сек^-1. В этом случае дифференциальное уравнение (3) удобнее записывать в виде

,

где T = 1/k.

При этом передаточная функция звена примет вид:

W(p)= . (5)

Величина T называется постоянной времени интегри­рующего звена.

 

 

 

Рис. 2. Передаточная функция и переходный процесс интегрирующего звена.

 

На рис. 2 представлен характер изменения выход­ной величины интегрирующего звена при подаче на его вход постоянной входной величины x_0вх. Тогда из уравнения (4) получим:

X_вых = ζ^-1[X_вых(p)] = ζ^-1[kx_0вх ] = kx_0вхt.

Примером интегрирующего звена может служить гидравлический исполнительный механизм (рис. 3,а), который находит широкое применение в современных системах регулирования. Входной вели­чиной для него является перепад давлений ΔP_вх= Р₁ – P₂, а выход­ной - перемещение ΔS_вых поршня.

 

Рис 3. Примеры интегрирующих звеньев.

 

Сила давления на поршень равна f_п = (P₀₁ – P₀₂)F, где F - эф­фективная площадь поршня.

Если пренебречь трением и инерцией поршня и связанных с ним масс, то можно считать, что это усиление целиком расходуется на преодоление внешней нагрузки, приложенной к поршню (сопротив­ление перемещению регулирую­щего органа, заслонки, шибера и т. п.):

f_в.н = (P₀₁ – P₀₂)F. (6)

При небольших отклонениях от состояния равновесия расходы жидкости через вентили В₁ и В₂ пропорциональны перепадам дав­лений на вентилях

Q₁=K₁(P₁ – P₀₁); Q₂=K₂(P₀₂-P₂). (7)

Так как Q₁ = Q₂, то решив уравнения (6) и (7), получим:

P₀₁ = . (8)

Поступление жидкости за бесконечно малый отрезок времени в левую полость исполнительного механизма при расходе Q₁ со­ставляет Q₁dt. За счет этого поршень переместится на величину dΔS_вых.

Так как объем поступившей жидкости равен приращению объема левой полости исполнительного механизма, то можно записать:

Q_ldt = FdΔS_вых.

или

.

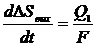Подставив из (7) значение Q₁, а из (8) значение Р₀₁, по­лучим:

.

В случае, если можно пренебречь величиной внешней нагрузки f_в.н, уравнение примет вид:

,

где

k =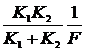

- коэффициент передачи интегрирующего звена, величину которого можно изменять в широких пределах с помощью вентилей В₁ и В₂.

Таким образом, дифференциальное уравнение гидравлического исполнительного механизма имеет вид (3) и, следовательно, в ди­намическом отношении он является интегрирующим звеном.

Другим примером интегрирующего звена может служить элек­тродвигатель постоянного тока Д (рис. 3,б) с независимым воз­буждением и малой электромеханической инерцией, если входной величиной является напряжение U_вх, а выходной - угол поворота якоря β_вых. В этом случае при изменении напряжения якоря на величину ΔU_вх изменение числа оборотов двигателя Δn в единицу времени будет пропорционально ΔU_вх:

Δn = K₁ ΔU_вх.

Увеличение угла поворота двигателя dΔβ_вых за бесконечно ма­лый отрезок времени dt пропорционально изменению числа оборотов за этот отрезок времени: dΔβ_вых = K₂Δndt, или d(Δβ_вых)/dt = K₂Δn.

Подставив значение Δn, получим дифференциальное уравнение интегрирующего звена:

.

Коэффициент передачи рассмотренного интегрирующего звена k = К₁К₂ может изменяться путем изменения величины напряжения U_о.в, подаваемого на обмотку возбуждения двигателя.

Апериодическое звено

Апериодическому звену соответствует дифференци­альное уравнение

. (9)

Перейдя к изображениям, получим:

ТрХ_вых(р) + Х_вых(р) = kX_вх(p).

Передаточная функция звена

W(p)= . (10)

Определим характер изменения выходной величины при подаче на вход в виде скачка входной величины x_0вх.

Дифференциальное уравнение (9) достаточно просто решается обычным методом. Однако в качестве примера найдем его решение через передаточную функ­цию звена.

По таблицам преобразования Лапласа находим изображение входной величины:

Х_вх(p) = ζ [x_0вх] = x_0вх/p.

Изображение выходной ве­личины

X_вых(p)=W(p)X_вх(p) (11)

или

X_вых(p) = .

Выразим оригинал функции x_вых через ее изображе­ние, вынеся постоянную величину за знак преобразо­вания Лапласа:

x_вых = ζ^-1[X_вых(p)] = .

Полагая 1/T = α, по таблицам преобразований Лапла­са находим:

x_вых=kx_0вх(1- ). (12)

 

 

Рис. 4. Передаточная функция и переходные про­цессы апериодического звена при различных значе­ниях постоянной времени.

 

Переходный процесс апериодического звена пред­ставлен на рис. 4. Кривые переходных процессов име­ют вид экспонент, т. е. время, необходимое для того, чтобы выходная величина x_вых достигла установившего­ся значения kx_0вх, теоретически бесконечно велико.

В связи с этим апериодическое звено часто называют инерционным звеном первого порядка.

Величина Т имеет размерность времени и называется постоянной времени. На рис. 4 представлены переход­ные процессы апериодического звена при различных значениях постоянной времени.

Из кривых переходного процесса ясен физический смысл постоянной времени звена. Она может быть определена как время, в течение которого выходная величи­на достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости изменения ее в начальный момент времени.

Постоянная времени определяет динамические свой­ства звена. Чем она больше, тем медленнее протекает переходный процесс в звене, и наоборот. В частности, при T = 0 процесс протекает в звене мгновенно и инерци­онное звено превращается в безинерционное усили­тельное.

Следует отметить также, что при t = T значение выходной ве­личины составляет 63% нового установившегося значения.

 

 

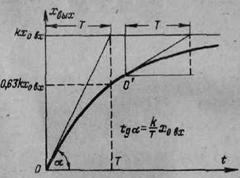
Рис. 5. Графическое определение по­стоянной времени апериодического звена.

 

Постоянная времени звена геометрически (рис. 5) опреде­ляется как проекция на ось вре­мени отрезка касательной к экс­поненте, заключенного между точкой касания и точкой пере­сечения касательной с линией установившегося значения выходной величины. Длина этой проекции одинакова для касательных, проведенных в любой точке экспоненты (точки O и O΄).

На рис. 6 приведены примеры апериодических звеньев. Вход­ной величиной этих звеньев является напряжение u_вх, а выход­ной - напряжение u_вых, снимаемое с конденсатора С.

 

Рис 6. Примеры апериодическихзвеньев

 

Согласно второму закону Кирхгофа для электрической цепи по рис. 6,а можно записать:

u_вх = iR₁ + u_вых; u_вых = ; u_вых = ,

откуда

; .

По первому закону Кирхгофа

.

Подставив значение i в выражение для u_вх, получим:

.

Преобразовав дифференциальное уравнение по Лапласу, полу­чим:

,

откуда находим передаточную функцию звена:

,

где

; .

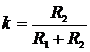Таким образом, электрическая цепь, изображенная на рис. 6,а, является апериодическим звеном.

Коэффициент передачи звена регулируется величинами сопро­тивлений R₁ и R₂. При этом пропорционально коэффициенту пере­дачи изменяется и постоянная времени.

При R₂=∞ получаем электрическую цепь по рис. 6,б. Коэффи­циент передачи, постоянная времени и передаточная функция в этом случае будут равны:

; ; .

Постоянная времени изменяется путем изменения величины со­противления R.

Электрическая цепь, представленная на рис. 6,б, является апе­риодическим звеном с коэффициентом передачи, равным единице.

Колебательное звено

Колебательное звено имеет дифференциальное урав­нение

. (13)

Передаточная функция звена

. (14)

Характер переходного процесса звена или соедине­ния, определяемого дифференциальным уравнением (13), зависит от расположения корней его характери­стического уравнения

(15)

на комплексной плоскости.

Корни характеристического уравнения (15)

(16)

С учетом (14), (11) и таблицы преобразований Лапласа, находим изображе­ние выходной величины:

. (17)

В зависимости от знака подкоренного выражения (16) при нахождении оригинала по его изображению (17) могут возникнуть три случая:

1. При T₁/T₂ > 2 оба корня характеристического урав­нения вещественные отрицательные: р₁ = - α₁, р₂ = - α₂. С учетом этого запишем выражение (17) в виде

.

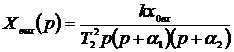По этому изображению согласно таблицы преобра­зований Лапласа находим оригинал:

. (18)

Таким образом, при T₁/T₂ > 2 переходный процесс оп­ределяется двумя экспонентами и в этом случае диф­ференциальное уравнение (13) характеризует переход­ные процессы соединения, состоящего из двух соединен­ных последовательно апериодических звеньев. Это видно также непосредственно из передаточной функции соеди­нения, если ее записать в виде

или

,

где T₃=1/α₁ и T₄=1/ α₂.

Следовательно, при T₁/T₂ > 2 нет необходимости вво­дить понятия нового типового звена, хотя на практике часто такое соединение называют инерционным звеном второго порядка.

2. При T₁/T₂ = 2 характеристическое уравнение имеет два одинаковых вещественных отрицательных корня

p₁ = p₂ = - α = - 1/T₂.

С учетом этого запишем выражение (17) в виде

.

По таблице преобразования Лапласа находим:

. (19)

Переходный процесс периодический. Так как при этом передаточная функция (14) может быть представлена в виде

,

где T = 1/α, то при T₁/T₂ = 2, так же как и при T₁/T₂> 2, нет необходимости вводить понятия нового типового звена.

3. При T₁/T₂< 2 характеристическое уравнение имеет два сопряженных комплексных корня

,

где

; . (20)

С учетом этого запишем выражение (17) в виде

. (21)

Обозначив в (21)

и ,

найдем оригиналы:

и .

Находим характер из­менения выходной величины звена:

,

или 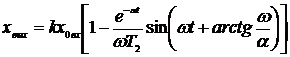. (22)

Таким образом, переходный процесс звена при T₁/T₂< 2, характеризуемый уравнением (22), периоди­чен и представляет собой затухающую синусоиду, ам­плитуда которой убывает от полупериода к полупериоду по экспонен­циальному закону . В этом случае звено нель­зя представить в виде соединения из других звеньев. В связи с этим элементарное звено, дина­мические качества кото­рого определяются диф­ференциальным уравне­нием (13), при T₁/T₂< 2 относится к типовым звеньям и называется колебательным звеном.Переходные процессы колебательного звена в зависимости от отношения T₁/T₂ представлены на рис. 7.

 

 

Рис. 7. Передаточная функция и переходные процессы колеба-тельного звена при различных значениях отношения постоянных времени.

 

Как следует из выражения (22), мнимая составляю­щая ω корней характеристического уравнения является круговой частотой колебательного звена. Период коле­баний Т = 2π/ω. Оценкой переходного процесса колеба­тельного звена служит степень затухания колебаний. Степенью затухания ψ называется отношение разности двух соседних амплитуд одного знака (взятых относи­тельно среднего положения kx_0вх) к первой из них (рис. 8,а):

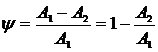. (23)

Как следует из рис. 8,а,

, .

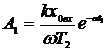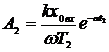Так как t₂ – t₁ = T, то подставив значения A₁ и A₂ в (23), получим:

. (24)

Чем ближе к единице величина ψ, тем быстрее зату­хают колебания переходного процесса.

 

 

Рис. 8. Переходные процессы колебательного звена при 1>ψ>0 и ψ = 0.

 

Степень затухания зависит от отношения веществен­ной составляющей комплексных корней характеристиче­ского уравнения α к их мнимой составляющей ω. В свою очередь это отношение определяется отношением посто­янных времени T₁/T₂:

.

4. При T₁ = 0 T₁/T₂ = 0 вещественная и мнимая со­ставляющие корней характеристического уравнения бу­дут равны:

; .

Подставив эти зна­чения в выражение (22) для переходного процесса колебательно­го звена, получим

. (25)

Такое колебатель­ное звено называется консервативным.

Переходный процесс будет в этом случае не­затухающим колеба­тельным (так как ψ = 0) с частотой ω₀ = 1/T₂, периодом T = 2πT₂ и амплитудой A=kx_0вх (рис.8,б).

Чем больше T₁ и меньше Т₂, тем больше степень затухания колебательного звена.

Следовательно, для уменьшения колебательности си­стем регулирования в колебательных звеньях необходи­мо увеличивать постоянную времени T₁ и уменьшать T₂. Однако это целесообразно делать лишь и определенных пределах, так как при чрезмерном увеличении отноше­ния T₁/T₂ переходный процесс затягивается (см. рис. 7) и время регулирования увеличивается.

На рис. 9 даны примеры колебательных звеньев.

Входной величиной мембранного пневматического клапана (рис. 9,а) является давление ΔР_вх, а выходной – перемещение ΔS_вых штока клапана (отсчет ве­дется в малых приращениях от равновесного состояния).

 

 

Рис. 9. Примеры колебательных звеньев.

 

Если нельзя пренебречь инер­цией подвижной системы клапана и силами трения, то условие равнове­сия сил, действующих на клапан, за­пишется как

.

Входное усилие при площади F мембраны равно:

.

Сила инерции f_и равна произве­дению массы m подвижной системы на ускорение a = d²(ΔS_вых)/dt²:

.

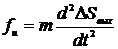Учитывая только силу вязкого трения, которая пропорциональна скорости перемещения подвижной системы, получим:

.

Сила противодействия пружины пропорциональна ее сжатию

,

где с - жесткость пружины.

Подставив значения сил в уравнение равновесия, получим:

.

В настоящее время принято составлять дифференциальные урав­нения звеньев в безразмерных (относительных) единицах.

Безразмерной единицей давления будем считать отношение ΔР_вх к максимальной величине давления Р_макс на мембрану, при котором клапан полностью закрывается; безразмерной единицей перемещения штока клапана примем отношение ΔS_вых к полному ходу S_макс

; ,

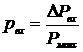откуда

; ;

.

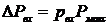Подставив эти значения в дифференциальное уравнение, полу­чим выражение его в безразмерных единицах:

.

С учетом того, что сS_макс = Р_максF, можно записать:

.

Таким образом, при учете инерции подвижной системы и вяз­кого трения мембранный пневматический клапан при b/ <2 яв­ляется колебательным звеном.

Постоянные времени и коэффициент передачи его равны:

; ; .

Из этого примера следует, что в элементах систем регулирования вязкое трение не всегда является нежелательным. В данном случае достаточно высокое вязкое трение обеспечивает устойчивую работу клапана, так как постоянная времени T₁ пропорциональна коэффи­циенту вязкого сопротивления b.

Практически, когда силы вязкого трения в механических элемен­тах недостаточны, применяют дополнительное демпфирование под­вижной системы, т. е. вводят дополнительную силу, противодействую­щую перемещению подвижной системы и пропорциональную скорости этого перемещения.

Если пневматический клапан применяется в системе с инерцион­ным объектом, в котором переходные процессы протекают медленно, т. е. скорости изменения р_вх и s_вых небольшие, то величина ускоре­ния d²S_вых/dt ² с точностью, достаточной для практических расче­тов, может быть принята равной нулю. Тогда дифференциальное уравнение клапана примет вид:

.

Следовательно, в этом случае можно пренебречь инерционностью подвижных частей пневматического клапана и представлять его в ди­намическом отношении как апериодическое звено с передаточной функцией; определяемой формулой (10).

Па рис. 9,б приведена электрическая схема, переходный про­цесс которой также описывается дифференциальным уравнением вто­рого порядка.

Постоянные времени и коэффициент передачи в этом случае равны:

;

;

.

При T₁/T₂< 2 схема представляется колебательным звеном. Все три параметра схемы выражаются через одни и те же величины че­тырех сопротивлений и двух емкостей. Это является ее недостатком, так как параметры настройки, определяющие динамические свойства звена, взаимозависимы. Поэтому установка оптимальной величины одного из трех параметров настройки в большинстве случаев не дает возможности получить оптимальные значения также для двух осталь­ных параметров. Кроме этого, такая настройка трудоемка и требует высокой квалификации наладчика.