Классификация точек разрыва функции

Точки разрыва I-го рода

def. Если функция f(x) в точке имеет конечные пределы слева и справа и если не все три числа равны между собой, то называется точкой разрыва I-го рода.

1) Если 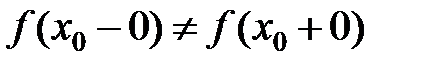, то в точке – конечный скачок.

x

x0

y

0

 

 

– точка разрыва I-го рода, конечный скачок.

 

 

2) Если или , а не определена, то в точке – устранимый разрыв.

x

x0

y

0

 

Если положить , то в точке восстановится непрерывность.

 

Точки разрыва II-го рода

def. Если в точке хотя бы один из односторонних пределов равен или не существует, то – точка разрыва II-го рода.

x

x0

y

0

– точка разрыва II-го рода.

 

 

Пример16.1.

 

 

Пример16.2.

 

 

Пример16.3.