Декартова система координат в пространстве












Основный принцип аналитической геометрии: соответствие
точка «набор чисел (координат)
Уравнение геометрического объекта (прямой, кривой, плоскости, поверхности) ¾ это такое уравнение  (или система из нескольких уравнений), что
(или система из нескольких уравнений), что
1) координаты произвольной точки объекта обращают уравнение в тождество;
2) если координаты некоторой точки удовлетворяют уравнению, то точка принадлежит данному объекту.
Векторная алгебра
Вектор – направленный отрезок прямой, то есть пара точек пространства, одна из которых объявляется началом, а вторая концом вектора.



Такой вектор называется приложенным.
Вектор – совокупность направленных отрезков пространства, которые можно перевести друг в друга параллельным переносом.
Такой вектор называется свободным (то есть его можно рассматривать как один направленный отрезок, который можно перемещать в пространстве, так, чтобы он оставался параллельным самому себе).




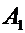

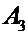
Координаты свободного вектора  есть координаты точки
есть координаты точки  вектора
вектора  , который получается из
, который получается из  переносом начала вектора
переносом начала вектора  в начало координат
в начало координат  .
.
Пусть  ,
, 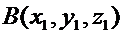 . Тогда
. Тогда
 .
.
 Длина вектора
Длина вектора 









По теореме Пифагора:
 ,
,
 .
.
Пример. Найти длину отрезка 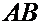 , где
, где  ,
,  .
.
 ,
,
 .
.
Операции над векторами
1) Сложение векторов (правило параллелограмма)






В координатах:

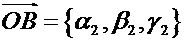
Тогда

2) Умножение на скаляр (число)




В координатах:
если 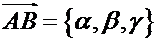 , то
, то 
Деление отрезка в заданном отношении
 Задача. Даны точки
Задача. Даны точки 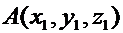 и
и  . Найти координаты точки
. Найти координаты точки  , принадлежащей отрезку
, принадлежащей отрезку 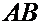 и такой, что
и такой, что 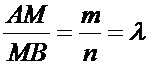
 .
.


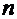



Имеем:  ,
,
откуда  .
.
Достаточно рассмотреть первую координату:
 Û
Û 
или, окончательно,
 ,
, 
Ответ: 
или 
Пример. Дан треугольник  с вершинами
с вершинами  ,
,  ,
,  . Найти длину медианы
. Найти длину медианы 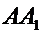 треугольника.
треугольника.
Координаты середины отрезка  находим по формуле деления отрезка с
находим по формуле деления отрезка с  :
:
 , откуда
, откуда 
Теперь  ;
;
 .
.
3) Скалярное произведение векторов
Пусть даны два вектора  и
и 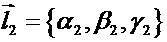 . Сопоставим им число
. Сопоставим им число  , называемое скалярным произведением и вычисляемое по правилу
, называемое скалярным произведением и вычисляемое по правилу

где  – угол между векторами.
– угол между векторами.



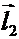
Свойства скалярного произведения:
а) симметричность 
б) однородность 
в) аддитивность 
Вычисление скалярного произведения в координатах.
Пусть  и
и 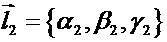 . тогда
. тогда
 .
.
Доказательство. Обозначим единичные базисные векторы, направленные по осям 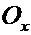 ,
,  , и
, и  через
через  ,
,  ,
,  соответственно. Тогда
соответственно. Тогда  ,
,  .
.
Заметим, что
 ,
,  ,
, 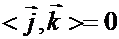 ,
,
 ,
,  ,
,  ,
,
поскольку эти векторы единичной длины и взаимно перпендикулярны.
Используя свойства 1-3 скалярного произведения, получаем:

Рассмотрим первое слагаемое:

Точно также доказывается, что второе слагаемое равно  , а третье
, а третье  . Ч.Т.Д.
. Ч.Т.Д.
Лекция 4
Пример. Дан треугольник  с вершинами
с вершинами  ,
,  ,
,  . Найти величину угла
. Найти величину угла  .
.
Имеем: 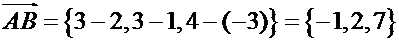 ;
;

Запишем формулу скалярного произведения:
 .
.
В координатах:
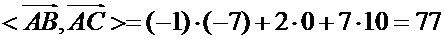 ,
,
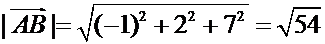 ,
,

Отсюда
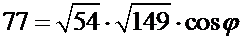 ,
,  ,
,  .
.
Критерий перпендикулярности
 Û
Û 
Пример. Дан треугольник  с вершинами
с вершинами  ,
,  ,
,  . Точка
. Точка 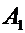 есть основание высоты, опущенной из вершины
есть основание высоты, опущенной из вершины  на сторону
на сторону  . Найти
. Найти  .
.



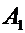

Положение точки 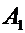 определяется двумя векторными соотношениями. 1) Так как точка
определяется двумя векторными соотношениями. 1) Так как точка 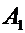 лежит на
лежит на  , то вектор
, то вектор  коллинеарен вектору
коллинеарен вектору  , то есть
, то есть 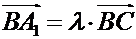 . 2) Поскольку
. 2) Поскольку 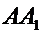 – высота, то вектор
– высота, то вектор  перпендикулярен вектору
перпендикулярен вектору  , то есть
, то есть  . Вектор
. Вектор  можно записать как сумму векторов
можно записать как сумму векторов  и
и  , то есть
, то есть  . Подставляя это соотношение в уравнение
. Подставляя это соотношение в уравнение  , получим уравнение на коэффициент
, получим уравнение на коэффициент  :
:
 Û
Û  ,
,
откуда
 .
.
В координатах:
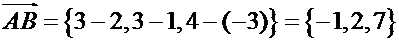 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

Теперь высота треугольника может быть найдена как длина вектора  :
:
 .
.
4) Векторное произведение векторов
Сопоставим произвольной паре векторов  ,
, 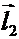 третий вектор
третий вектор  , удовлетворяющий трем условиям:
, удовлетворяющий трем условиям:
а) вектор  перпендикулярен к плоскости, натянутой на вектора
перпендикулярен к плоскости, натянутой на вектора  и
и 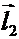 ;
;
б) длина  равна площади параллелограмма
равна площади параллелограмма  , натянутого на вектора
, натянутого на вектора  и
и 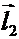 ;
;
в) если смотреть с конца стрелки вектора  на плоскость, образованную векторами
на плоскость, образованную векторами  и
и 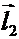 , то вращение (внутри
, то вращение (внутри  ) от
) от  к
к 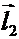 должно происходить против часовой стрелки.
должно происходить против часовой стрелки.
 |

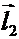

Нетрудно видеть, что если векторы  и
и 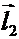 независимы (то есть
независимы (то есть  ), то вектор
), то вектор  определен условиями 1-3 однозначно. Если векторы
определен условиями 1-3 однозначно. Если векторы  и
и 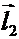 зависимы, то можно по определению считать, что вектор
зависимы, то можно по определению считать, что вектор  равен 0. Векторное произведение векторов
равен 0. Векторное произведение векторов  и
и 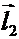 обозначается как
обозначается как  .
.
Свойства векторного произведения.
1) 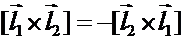 (антикоммутитивность)
(антикоммутитивность)
2) 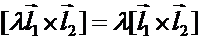 (однородность)
(однородность)
3)  (аддитивность)
(аддитивность)
Вычисление векторного произведения в координатах.
Даны векторы  ,
, 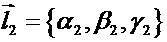 , тогда
, тогда
 .
.
Доказательство основано на трех соотношениях
 ,
,  ,
, 
(которые следуют непосредственно из определения векторного произведения) и преобразовании выражения
 ,
,
аналогичному тому, которое было проведено при выводе формулы скалярного произведения векторов в координатах.
Ч.Т.Д.
Мнемоническая формула векторного произведения:

Пример. Найти площадь треугольника  с вершинами
с вершинами 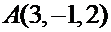 ,
,  ,
,  .
.
Решение. Воспользуемся вторым свойством векторного произведения: длина  равна площади параллелограмма, натянутого на векторы
равна площади параллелограмма, натянутого на векторы  ,
,  . Таким образом, нам нужно найти
. Таким образом, нам нужно найти  и затем положить
и затем положить  .
.
Имеем:  ,
,
 ,
,

 .
.
5) Смешанное произведение векторов
Произвольной тройке векторов  ,
, 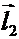 ,
,  сопоставим число, равное
сопоставим число, равное  и называемое смешанным произведением векторов. Обозначается смешанное произведение через
и называемое смешанным произведением векторов. Обозначается смешанное произведение через  . Из формулы разложения определителя по строке следует, что
. Из формулы разложения определителя по строке следует, что
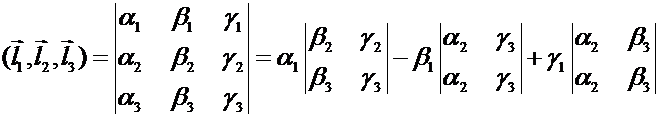
 Геометрический смысл смешанного произведения
Геометрический смысл смешанного произведения





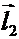
Из рисунка видно, что, с точностью до знака, смешанное произведение равно объему параллелепипеда, натянутого на векторы  ,
, 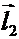 ,
,  :
:
 .
.
Следствие: критерий компланарности векторов. Три вектора  ,
, 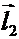 ,
,  компланарны (то есть параллельны одной плоскости) тогда и только тогда когда
компланарны (то есть параллельны одной плоскости) тогда и только тогда когда  .
.
Пример. Найти объем пирамиды 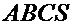 с вершинами
с вершинами  ,
, 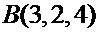 ,
,  ,
,  .
.
Решение.
Объем пирамиды вычисляется по формуле  , а объем параллелепипеда по формуле
, а объем параллелепипеда по формуле 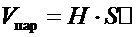 .
.
Следовательно,  и
и  . Остается вычислить смешанное произведение векторов
. Остается вычислить смешанное произведение векторов  . Имеем
. Имеем
 ,
,
 ,
,
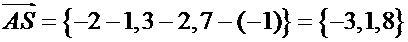 .
.
Теперь вычисляем смешанное произведение в координатах:


Окончательно, 
Аналитическая геометрия на плоскости
Векторное уравнение прямой




Пусть известны координаты некоторой точки  прямой
прямой  и координаты направляющего вектора
и координаты направляющего вектора  . Точка
. Точка  лежит на прямой
лежит на прямой  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы  и
и  коллинеарны, то есть
коллинеарны, то есть 
с некоторым коэффициентом пропорциональности  .
.
Параметрическое уравнение прямой.
Запишем векторное уравнение прямой в координатах:

Полученную систему называют параметрическим уравнением прямой.
Пример. Написать параметрическое уравнение прямой 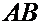 , где
, где  ,
,  .
.
Направляющий вектор прямой есть
 .
.
В качестве точки на прямой возьмем точку  . Подставляя эти данные в параметрическое уравнение прямой, получим
. Подставляя эти данные в параметрическое уравнение прямой, получим
 Û
Û 
Это уравнение определяет прямую.
При  получаем
получаем  ,
,  , то есть это — точка
, то есть это — точка  . Значению
. Значению  отвечает точка
отвечает точка  , значению
, значению  ¾ точка, находящаяся в середине отрезка
¾ точка, находящаяся в середине отрезка  . Значению
. Значению  отвечает точка, расположенная симметрично точке
отвечает точка, расположенная симметрично точке  относительно
относительно  .
.







Зная координаты произвольной точки плоскости, по параметрическому уравнению можно определить, лежит ли данная точка на прямой и, если да, то какому значению эта точка отвечает. Например, для точки  получаем
получаем
 Û
Û 
Система противоречива, и точка  не лежит на прямой. Для точки
не лежит на прямой. Для точки  получаем
получаем
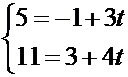 Û
Û  ,
,
откуда следует, что  лежит на прямой и отвечает значению
лежит на прямой и отвечает значению  .
.
Каноническое уравнение прямой.
Выражая параметр  из каждого уравнения параметрической системы, получим
из каждого уравнения параметрической системы, получим
 Û
Û 
Опуская  , получим окончательно:
, получим окончательно: 
Пример. Дано каноническое уравнение прямой

Через какую точку и в каком направлении проходит данная прямая?
Вспомним, что в числителе в каноническом уравнении стоит точка прямой, а в знаменателе – ее направляющий вектор. Таким образом,  ,
, 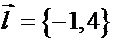 .
.
Пример. Написать уравнение прямой, проходящей через точку  , перпендикулярно прямой
, перпендикулярно прямой  .
.
Уравнение любой прямой начинается с выписывания шаблона

В числитель следует подставить координаты какой-либо точки прямой, а в знаменатель – координаты направляющего вектора. Точка известна -  , поэтому:
, поэтому:
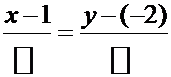
Направляющий вектор должен быть перпендикулярен прямой  , и, в частности, перпендикулярен ее направляющему вектору
, и, в частности, перпендикулярен ее направляющему вектору  . Воспользуемся критерием перпендикулярности векторов и подберем вектор
. Воспользуемся критерием перпендикулярности векторов и подберем вектор  , скалярное произведение которого с вектором
, скалярное произведение которого с вектором  равно 0. Самый простой способ – взять в качестве
равно 0. Самый простой способ – взять в качестве  вектор
вектор  (то есть переставить координаты
(то есть переставить координаты  и изменить знак у одной из координат). Таким образом, каноническое уравнение искомой прямой имеет вид
и изменить знак у одной из координат). Таким образом, каноническое уравнение искомой прямой имеет вид
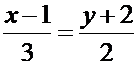 .
.
Общее уравнение прямой.
В каноническом уравнении избавимся от знаменателей и перенесем все члены по одну сторону от знака равенства. Имеем:
 Û
Û 
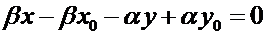 Û
Û 
Переобозначая коэффициенты полученного уравнения, получим  ,
,
где  ,
,  ,
,  .
.
Отметим, что направляющий вектор прямой равен  и, следовательно, равен
и, следовательно, равен 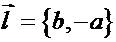 .
.
Скалярное произведение вектора с направляющим вектором  равно 0, поэтому
равно 0, поэтому  - вектор нормали к прямой.
- вектор нормали к прямой.
Пример. Дан треугольник  с вершинами
с вершинами  ,
,  ,
,  . Написать уравнение высоты
. Написать уравнение высоты 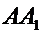 .
.
Решение. Уравнение высоты имеет вид

Здесь  – вектор нормали к
– вектор нормали к 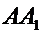 . В частности,
. В частности,  , поэтому
, поэтому  .
.
 .
.
Остается найти константу  , для чего подставим в данное уравнение координаты точки
, для чего подставим в данное уравнение координаты точки  . Получаем
. Получаем

откуда  , и уравнение прямой имеет вид
, и уравнение прямой имеет вид  .
.
Приведенное уравнение прямой.
Рассмотрим общее уравнение прямой  , и в случае
, и в случае  выразим переменную
выразим переменную  через остальные члены уравнения.
через остальные члены уравнения.  .
.
После переобозначений получаем так называемое приведенное уравнение прямой  .
.
Геометрический смысл коэффициента 
в приведенном уравнении.
Пусть для простоты  ,
, 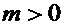 .
.













Рассмотрим угол  , образованный прямой и положительным направлением оси абсцисс. Из рисунка видно, что
, образованный прямой и положительным направлением оси абсцисс. Из рисунка видно, что
 .
.
Таким образом,  есть тангенс угла наклона прямой к оси
есть тангенс угла наклона прямой к оси 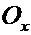 .
.
Угол между прямыми.
Пусть заданы две прямые  и
и  . Задача – найти угол между ними.
. Задача – найти угол между ними.
 |





Из рисунка видно, что
 ,
,
где 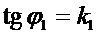 ,
,  .
.
Воспользуемся формулой
 .
.
Отсюда
 .
.
Окончательный ответ:
 .
.
В частности, если угол составляет  , то
, то  . Это возможно, если
. Это возможно, если 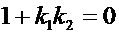 . Получаем критерий перпендикулярности прямых.
. Получаем критерий перпендикулярности прямых.
 .
.
Лекция 1.6
Пример. Дан треугольник  с вершинами
с вершинами  ,
,  ,
,  . Написать уравнение биссектрисы
. Написать уравнение биссектрисы 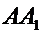 .
.
Решение. Найдем приведенные уравнения прямых 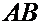 ,
,  . Для
. Для 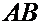 имеем точку
имеем точку  , и направляющий вектор
, и направляющий вектор  , откуда следует каноническое уравнение прямой
, откуда следует каноническое уравнение прямой
 Û
Û
 Û
Û  .
.
Аналогично, для  имеем точку
имеем точку  и направляющий вектор
и направляющий вектор  , откуда каноническое уравнение прямой имеет вид
, откуда каноническое уравнение прямой имеет вид
 Û
Û
 Û
Û  .
.
Напишем приведенное уравнение биссектрисы 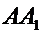 в общем виде:
в общем виде:
 .
.


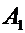




Найдем  сначала из приведенных уравнений прямых
сначала из приведенных уравнений прямых 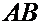 и
и 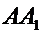 , а затем из уравнений
, а затем из уравнений  и
и 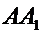 . Получаем:
. Получаем:
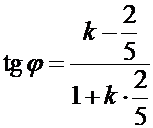 ,
, 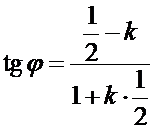 ,
,
откуда
 Û
Û 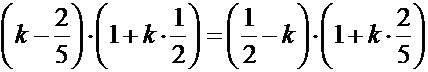 Û
Û  ,
,
и, следовательно,
 , Û
, Û  .
.
Одно из значений  , а именно
, а именно  (это видно из рисунка), отвечает биссектрисе смежного угла с углом
(это видно из рисунка), отвечает биссектрисе смежного угла с углом 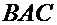 . Поэтому
. Поэтому  . Остается определить значение
. Остается определить значение  в уравнении биссектрисы
в уравнении биссектрисы  . Подставляя координаты точки
. Подставляя координаты точки  , получим
, получим
 Û
Û  .
.
Ответ:  .
.
Аналитическая геометрия в пространстве
Прямая в пространстве.
Прямая в пространстве определяется произвольной точкой на ней и направлением, которое задается произвольным вектором, параллельным данной прямой.




Условие, что точка  лежит на данной прямой, в векторной форме запишется в виде условия коллинеарности векторов
лежит на данной прямой, в векторной форме запишется в виде условия коллинеарности векторов  и
и  :
:
 .
.
Запишем данное равенство покоординатно, получим параметрическое уравнение прямой.

Выражая  из каждого из трех уравнений системы, получим каноническое уравнение прямой:
из каждого из трех уравнений системы, получим каноническое уравнение прямой:

Пример. Написать каноническое уравнение прямой, проходящей через точки  и
и  .
.
Решение. Направляющий вектор прямой – это вектор
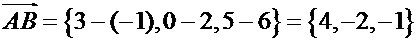 .
.
Подставляя в шаблон канонического уравнения в числитель координаты точки  , а в знаменатель - координаты вектора
, а в знаменатель - координаты вектора  соответственно, получим:
соответственно, получим:
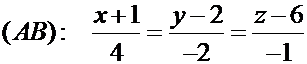 .
.
Первое уравнение плоскости.
Предположим, что нам известны координаты некоторой точки плоскости и координаты двух неколлинеарных векторов, параллельных данной плоскости.




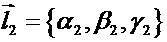
Тогда условие, что точка  лежит в данной плоскости сводится к условия, что три вектора:
лежит в данной плоскости сводится к условия, что три вектора:  ,
, 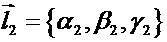 и
и  параллельны этой плоскости, или, иначе, эти три вектора компланарны. Критерием компланарности векторов было равенство нулю их смешанного произведения:
параллельны этой плоскости, или, иначе, эти три вектора компланарны. Критерием компланарности векторов было равенство нулю их смешанного произведения:
 .
.
В координатной записи это дает первое уравнение плоскости:
 .
.
Пример. Написать уравнение плоскости, проходящей через точки  ,
,  и
и  .
.
Решение. Найдем два вектора, параллельных плоскости  .
.
 ,
,
 .
.
В качестве точки плоскости подставим уравнение координаты точки  . Получим
. Получим

Раскрывая определитель по первой строке, получим:
 ,
,
откуда
 .
.
Раскрывая скобки и приводя подобные, получим окончательно:
 Û
Û 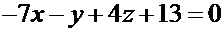
Второе уравнение плоскости.
Пусть заданы координаты некоторой точки  плоскости и координаты вектора
плоскости и координаты вектора  , перпендикулярного к плоскости.
, перпендикулярного к плоскости.




Теперь условие, что точка лежит в данной плоскости, сводится к взаимной перпендикулярности векторов  и
и  :
:
 .
.
Переходя к координатной записи, получим:
 .
.
Это – второе уравнение плоскости.
Пример. Дана точка  и прямая
и прямая
 .
.
Написать уравнение плоскости  , проходящей через точку
, проходящей через точку  перпендикулярно к прямой
перпендикулярно к прямой  .
.
Решение. Направляющий вектор  прямой
прямой  является одновременно перпендикуляром к плоскости
является одновременно перпендикуляром к плоскости  . Поэтому
. Поэтому
 ,
,
откуда  .
.
В качестве приложения выведем формулу для расстояния от точки до плоскости. Пусть дана точка  и плоскость
и плоскость  . Требуется определить расстояние от
. Требуется определить расстояние от  до
до  .
.
Решение. Выпишем уравнение прямой  , проходящей через точку
, проходящей через точку  перпендикулярно к плоскости
перпендикулярно к плоскости  . Затем найдем координаты точки
. Затем найдем координаты точки  - точки пересечения прямой
- точки пересечения прямой  и плоскости
и плоскости  . После этого расстояние от
. После этого расстояние от  до
до  найдем как длину вектора
найдем как длину вектора  .
.
Имеем:

откуда
 .
.
В частности, если  - координаты точки
- координаты точки  , то они удовлетворяют уравнению плоскости
, то они удовлетворяют уравнению плоскости
 ,
,
откуда
 .
.
После приведения подобных слагаемых получим:
 .
.
Следовательно, вектор  имеет координаты
имеет координаты

Остается о
 2018-01-21
2018-01-21 1504
1504







