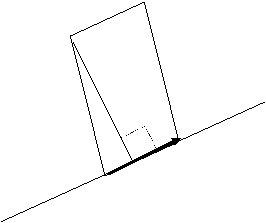
Расстояние от точки до прямой

Расстояние от точки до прямой совпадает с высотой параллелограмма, построенного на векторах и . .

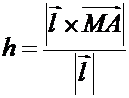
ПРИМЕР. Найти расстояние от точки до прямой

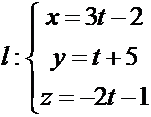
РЕШЕНИЕ.

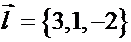
Найдем векторное произведение

Задача 1. Прямая является пересечением двух плоскостей и , заданных уравнениями и . Написать каноническое уравнение прямой .

РЕШЕНИЕ. Выпишем решение вырожденной системы

уравнений

в параметрической форме. Применим метод последовательных исключений Гаусса.

Обозначая , получим

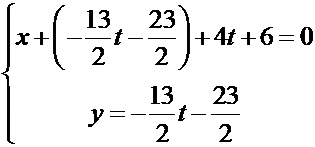
И окончательно

Эту систему уравнений можно интерпретировать как параметрическое уравнение прямой . Тогда точка, через которую проходит прямая – эта точка (отвечает значению ), а координатами направляющего вектора прямой являются коэффициенты при в каждом из трех уравнений системы, то есть 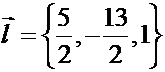. Таким образом, каноническое уравнение прямой имеет вид

Задача 2. Даны плоскость и точка . Найти точку , симметричную относительно плоскости .

РЕШЕНИЕ. Точка находится на прямой, проходящей через перпендикулярно к плоскости , причем лежит по другую сторону от плоскости и на том же расстоянии, что и . Другими словами, точка - середина отрезка , принадлежит плоскости . Уравнение прямой имеет вид

Если координаты точки обозначить как , то координаты точки можно найти по формуле деления отрезка в данном отношении:

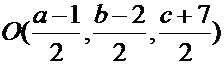Следовательно, координаты 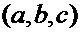точки удовлетворяют системе уравнений

Положим ,

тогда .

Подставляя эти выражения во второе уравнение системы, получим

Умножив на 2, раскрыв скобки и приведя подобные слагаемые, получим

Û .

Следовательно,

Ответ: .

Задача 3. Дана точка прямая

и прямая

Найти уравнение прямой , проходящей через точку перпендикулярно к прямой и пересекающей прямую .

РЕШЕНИЕ. Имеется целая плоскость , целиком заполненная прямыми, проходящими через точку и перпендикулярными к прямой . Чтобы найти в ней нужную нам прямую, достаточно найти пересечение плоскости и прямой .

Уравнение плоскости имеет вид:

Û .

Пересечение плоскости и прямой определяется из системы уравнений:

Из последнего уравнения получаем:

Подставляя эти соотношения в первое уравнение системы, получим:

Û .

Следовательно, и координаты точки имеют вид

Направляющий вектор искомой прямой есть

Каноническое уравнение прямой имеет вид

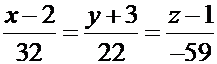Лекция 8

Математический анализ

Предел функции одного вещественного

переменного .

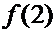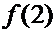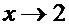Как вычислить значение функции при , при , при ? Непосредственное вычисление громоздко и, возможно, даст большую погрешность при округлении. Однако, можно попробовать найти , и затем оценить, насколько сильно уклоняется от . Если уклонение тем меньше, чем меньше разность , то естественно считать, что , а “в пределе” при значение точно равно .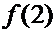

Действительно,

Таким образом, значения функции в точках, мало отличающихся от 2, мало отличается от 4. Можно сказать, что 4 есть предел функции при .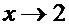

Определение. Число называется пределом функции в точке и обозначается как

если для любого найдется такое число , что при всех .

Свойства пределов.

1. .

2. .

3. Если , то .

Лемма о двух милиционерах.

Если и , то .

Определение. Функция называется непрерывной в точке , если .

Теорема. Если функция непрерывна в точке , а функция непрерывна в точке , то композиция непрерывна в точке и .

Попробуем вычислить при . Подставим значение в качестве аргумента функции . Получим - “неопределенное” выражение. Какое число в этом случае определяет приближенное значение функции ? Чтобы это определить, следует “разрешить особенность” функции в точке , иными словами, определить, за счет чего числитель и знаменатель дроби обращаются в ноль при подстановке 1 вместо . Имеем:

Следовательно,

Пример.

Вновь непосредственный подсчет приводит к неопределенности:

Числитель можно разложить на множители

Преобразуем знаменатель, домножив и числитель, и знаменатель дроби на сопряженное выражение - сумму :

Теперь

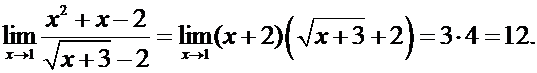
Первый замечательный предел.

Рассмотрим предел

Прямое вычисление дает:

Для вычисления предела воспользуемся леммой о двух милиционерах.

Напишем неравенство для площадей треугольника , углового сектора и треугольника :

Поделим все на (поскольку функция четная, то можно считать, что ):

откуда

Следовательно,

Полученная формула называется первым замечательным пределом.

Пример. Вычислить предел

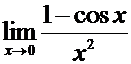
Решение.

Окончательно,

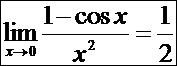
Предел функции на бесконечности.

Определение. Число называется пределом функции при , если для любого найдется такое число , что при всех .

Обозначается этот предел как

Если в определении предела считать, что или , то получится определение одностороннего предела или соответственно.

Очевидные пределы

Пример. Вычислить предел

Решение. Разделим и числитель и знаменатель на старшую степень . Имеем:

Пример. Вычислить предел

Решение.

При получаем

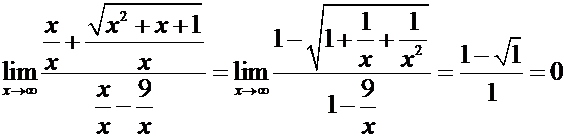
Второй замечательный предел.

Теорема (без доказательства). Предел монотонно возрастающей ограниченной функции (то есть и для произвольных ) существует и удовлетворяет неравенству .

Доказательство существования. Рассмотрим сначала функцию при натуральных значениях аргумента .

Покажем, что функция монотонно возрастает. Воспользуемся формулой бинома Ньютона

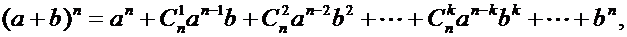где

(в числителе столько же множителей, сколько их имеется в знаменателе). Всего в формуле бинома слагаемых. Доказывается формула бинома индукцией по .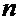

Разложим по формуле бинома выражения и .

Докажем неравенство . Имеем:

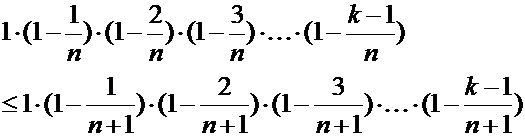
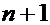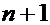Теперь неравенство становится очевидным (каждый множитель слева не больше соответствующего по порядку множителю справа). Следовательно, уже первые слагаемые в разложении больше суммы всех слагаемых в разложении , то есть

Покажем, что последовательность ограничена и не превосходит 3. Воспользуемся оценкой

откуда

Сумма оценивается сверху суммой геометрической прогрессии

откуда для любого 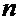. По теореме о пределе монотонной ограниченной функции существует предел при натуральных значениях переменной 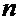. Этот предел был назван числом и может быть вычислен с любой степенью точности.

Для доказательства существования предела при произвольных вещественных можно воспользоваться очевидным неравенством

при ,

и теоремой о двух милиционерах, с учетом того, что

Можно показать, что предел существует и равен и при .

Пример. Вычислить предел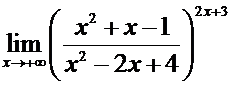

Решение.

Лекция 9

Следствия 1) ,

2) .

Доказательство. 1) Полагая в формуле , получим . Вычисляя натуральный логарифм от правой и левой частей формулы, получим

Û .

2). Полагая Û , получим .

Комбинирование пределов.

Пример. Вычислить предел

Решение. Это неопределенность вида . Действительно,

откуда .

Выполним тождественное преобразование

и воспользуемся формулой

Следовательно,

Сделаем замену .

Очевидно, что при . При этом , откуда . Получаем:

Непрерывность и типы разрывов.

Если или предела вообще не существует, то говорят, что функция имеет разрыв в точке . Всего имеется три типа разрывов.

1) Устранимый разрыв, когда существует , но .

Пример. Доопределим функцию при значением . Поскольку , то функция окажется разрывной в точке . Однако, изменив значение функции всего в одной точке, мы получим в результате непрерывную функцию, то есть мы устраним разрыв.

2) Разрыв 1-го рода. Если существует предел слева и предел справа , но , то говорят, что функция имеет разрыв первого рода с точке .

Пример. Рассмотрим функцию и точку . Имеем

При предел отличается знаком:

Таким образом, точка является точкой разрыва первого рода функции .

3) Все остальные разрывы считаются разрывами 2-го рода.

Пример 1. , .

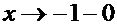Если , то . Если , то .

Пример 2. , 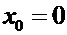. Если и при этом , , то 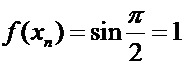. Если , но , , то тогда . Таким образом никакого предела (ни справа, ни слева) у функции в точке 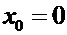нет.

Производные.

Определение. Число называется производной функции в точке , если существует предел

(предел отношения приращения функции в точке к приращению аргумента ).

Производная обозначается как 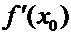или как .

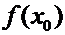
Для секущей графика (прямой, соединяющий точки и ) дробь 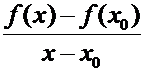равна угловому коэффициенту прямой

Здесь обозначают координаты текущей точки секущей. Таким образом, показывает, насколько плавно (гладко) изменяется секущая при .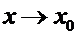

Определение. Касательная к графику функции в точке есть предельное положение секущих при .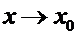

Из определения следует, что уравнение касательной есть

Геометрический смысл производной состоит в том, что она является угловым коэффициентом касательной к графику функции в точке .

Физический смысл производной. Пусть есть время, в течение которого материальная точка двигается вдоль прямой, а обозначает расстояние до некоторой точки отсчета . Тогда функция есть закон движения и определяет изменение положение точки со временем.

При такой интерпретации есть расстояние, которое проходит материальная точка за время . Следовательно, дробь 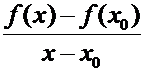есть средняя скорость движения за время . Переходя к пределу при 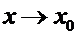, получаем, что 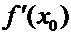есть мгновенная скорость движения, описываемого законом . Это и есть физический смысл производной.

Лекция 10.

Простейшие свойства производных.

Свойства пределов определяют следующие свойства производных.

2) для произвольной константы .

3) Если производная в точке существует, то функция непрерывна в этой точке.

Производные по определению.

Пример 1. .

То есть

Пример 2. .

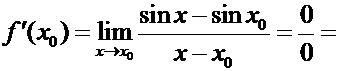
Таким образом,

Пример 3. .

Таким образом,

Таблица производных от элементарных функций.

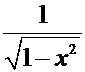
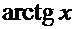
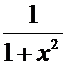
Рассмотрим дифференцирование степенной функции при некоторых .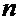

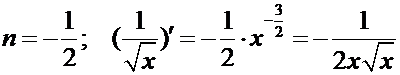
Имеется два основных приема дифференцирования функций

1) Формуладифференцирования произведения и частного двух функций

Доказательство. Докажем формулу дифференцирования произведения. По определению производной имеем:

2) Формула дифференцирования композиции (или сложной функции)

Доказательство По определению производной имеем:

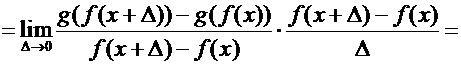
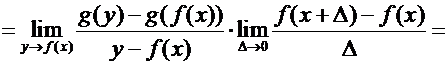
Примеры.

1^°)

2^°)

3^°)

4^°)

5^°)

6^°)

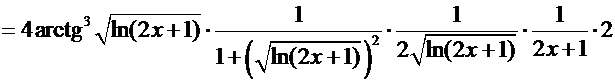
Логарифмическая производная.

Рассмотрим функцию .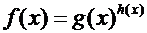

Теорема.

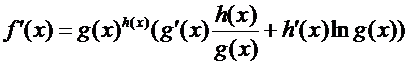Доказательство. Прием, с помощью которого мы найдем производную функцию , называется логарифмическим дифференцированием. Именно, прологарифмируем тождество , а затем найдем производную от правой и левой части.

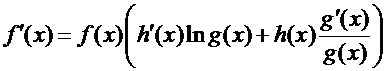Ч.Т.Д.

Пример.

откуда .

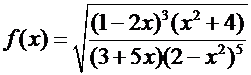
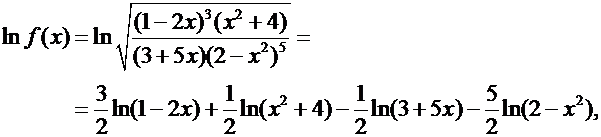
Производной обратной функции.

Определение. Функция называется обратной к функции если , .

Примеры.

1) , ;

2) , ;

3) , .

Теорема. Если есть обратная функция к функции , то

Доказательство. Используя формулу для дифференцирования сложной функции, продифференцируем тождество

Получаем:

Û , Ч.Т.Д.

Пример. Найдем производную функции . По теореме о производной обратной функции имеем:

где .

В силу основного тригонометрического тождества,

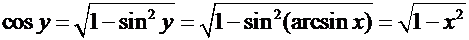Следовательно,

Лекция 11.

Производная функции, заданной параметрически.

Пример. Циклоида.

Длина пройденного пути равна, с одной стороны, , а с другой стороны, (длина дуги). Следовательно,

Обозначая 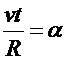, получим

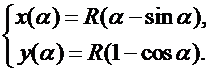
Функция, обратная к функции , не может быть выражена через элементарные функции. Поэтому явное представление также не может быть получено в классе элементарных функций.

Пусть есть параметрическое представление функции .

Теорема.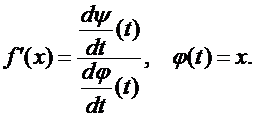

Доказательство. Пусть - функция, обратная к функции . Тогда , поэтому

По теореме о производной обратной функции имеем , где . Следовательно,

. Ч.Т.Д.

Производная неявной функции.

Иногда функцию можно задать неявно, посредством некоторого уравнения, зависящего от переменных и : .

В таком случае говорят, что функция задана неявно.

Пример 1. Û .

Однако в явном виде выразить функцию посредством элементарных функций можно не всегда.

Пример 2. .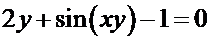

Пусть точка принадлежит множеству решений уравнения (то есть ), и пусть - некоторая функция, удовлетворяющая условию . Как найти производную 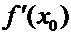? Проще всего продифференцировать тождество и, убедившись, что производная входит в получившееся выражение линейно, найти значение .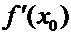

Продолжение примера 1.

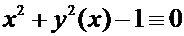Û , откуда

В частности, если

, то .

Проверка: , При получаем .

Основные теоремы

дифференциального исчисления.

Определение. Точка называется точкой локального минимума функции , если для всех из некоторого интервала выполнено соотношение

Если неравенство заменить на неравенство 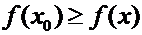, то точка будет называться точкой локального максимума функции .

Теорема Ферма. Пусть функция определена на некотором интервале и дифференцируема в точке . Тогда, если является точкой локального минимума или максимума функции , то