2018-01-21
1333
Экспериментальной основой расчетов за пределами упругости являются испытания в условиях одноосного растяжения. Диаграмма растяжения такого пластичного материала, как малоуглеродистая сталь, имеет следующий вид. Некоторые стали, сплавы, цветные металлы обладают, в достаточной мере, пластическими свойствами, но площадка текучести у них отсутствует.
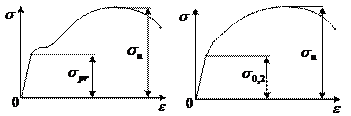
Реальные диаграммы весьма сложны для расчета. Чтобы упростить задачу их схематизируют, т.е. заменяют отрезками прямых или кривых, имеющих простое математическое описание. В зависимости от вида реальных диаграмм возможны разные пути схематизации. Приведем некоторые из них.
1) Схематизация диаграммой с площадкой текучести и линейным упрочнением. Напряжения и деформации здесь связаны следующими зависимостями:
1) при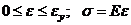 
(закон Гука)
2) при 
3) при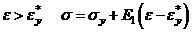 
Здесь 
- модуль упругости 
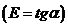
- модуль упрочнения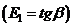 
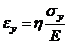- деформация, соответствующая пределу текучести.
- деформация, соответствующая началу упрочнения.
Участок упрочнения можно описать степенной кривой, лучше
приближающей соответствующий участок реальной диаграммы. Тогда мы получим диаграмму с площадкой текучести и степенным упрочнением. Связь между напряжениями и деформациями на последнем участке в этом случае выглядит
При 
, где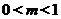 
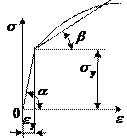2) Диаграмма с линейным упрочнением. Она используется в том случае, если схематизируемая диаграмма не имеет площадки текучести.
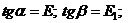
Связь между напряжениями и деформациями в этом случае очевидна. Разумеется. Что закон упрочнения и в этом случае можно принять степенным.
Однако, чаще всего мы будем использовать диаграмму идеального упруго-пластического материала, согласно которой материал вплоть до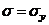 
идеально упруг (следует закону Гука), а затем идеально пластичен. Эту диаграмму можно рассматривать как частный случай предыдущей при модуле упрочнения равном нулю. Она используется в случае, когда материал имеет развитую площадку текучести либо в случае, когда она достаточно точно аппроксимирует реальную диаграмму.
