Геометрические характеристики поперечных сечений

 

При расчетах элементов инженерных конструкций приходится сталкиваться с необходимостью вычисления различных геометрических характеристик. Мы видим, что сила, которую может выдержать стержень на растяжение, пропорциональна площади поперечного сечения. Однако, площадь поперечного сечения не является исчерпывающей характеристикой. Сечения разной конфигурации могут иметь одинаковую площадь, но их поведение при изгибе или кручении будет различным. Простейший пример: полоса металла или бумаги, будучи согнутой (угловое сечение) приобретает способность сопротивляться изгибу в гораздо большей мере, чем такая же плоская полоса.

Для того, чтобы охарактеризовать геометрические свойства поперечных сечений стержней при таких нагружениях как изгиб, кручение и их комбинации, необходимо ввести более сложные характеристики – моменты площадей.

Рассмотрим произвольное поперечное сечение с площадью А. Выберем пока что произвольную систему координат и любым способом разобьем площадь сечения на элементы. Если площадь произвольного элемента умножить на его координату то мы получим элементарный момент первого порядка.

Суммируя элементарные моменты по площади сечения А, и беря предел полученной интегральной суммы, получаем:

- статический момент площади А относительно оси x.

Аналогично можно ввести статический момент относительно оси y:

. Подобным же путем можно получить еще три момента второго порядка

; ;

Первые две величины называют осевыми моментами инерции соответственно относительно осей x и y.

- центробежный момент инерции относительно осей х и у.

Составим еще один интеграл , который называ-

ется полярным моментом инерции. Очевидно, что, т.к.

то , т.е. полярный момент инерции равен сумме осевых.

Обратим внимание на очевидный факт: осевые моменты инерции и полярный момент инерции 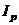всегда положительны, а статические моменты и центробежный момент инерции могут принимать как положительные, так и отрицательные значения.

Отметим еще некоторые свойства моментов:

1) момент (любой из моментов) составной площади равен сумме моментов ее частей.

2) Если фигура ограничена двумя замкнутыми контурами, то ее момент можно вычислить, вычитая из момента площади, ограниченной внешним контуром, момент площади ограниченной внутренним контуром.

3) Если хотя бы одна из осей является осью симметрии, то центробежный момент инерции относительно данных осей равняется нулю.

Это очевидно, т.к. фигуру можно представить как множество пар элементарных площадок, имеющих равными одну из координат и равными по величине и противоположными по знаку другую.

 

Статические моменты.

 

На основании теоремы Вариньена (о моменте равнодействую-

щей) можно записать

где 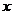и - координаты центра тяжести площади. Отсюда мы имеем

прием для отыскания центра тяжести площади: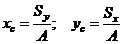

Ось, относительно которой статический момент равен нулю, называют центральной (естественно, что она проходит через центр

тяжести фигуры).

Если мы имеем дело с составной фигурой, т.е. фигурой состоящей из частей, для каждой из которой мы знаем площадь и координаты центра тяжести, то статические моменты можно найти:

где - соответственно площадь и координаты центра тяжести фигуры составляющей.