Рассмотрим стержневые системы, т.е. системы, составленные из стержней посредством связей. Если система содержит жесткие узлы, то ее называют рамой, а если все стержни в узлах соединены шарнирно, то фермой.
Следует отдавать отчет, что в реальных конструкциях нет ни абсолютно жестких узлов, ни идеальных шарниров. Реальные узлы всегда в той или иной мере податливы и в то же время обладают жесткостью и а зависимости от обстоятельств, выбирая расчетную схему, их полагают либо жесткими, либо податливыми. То же самое можно сказать и об спорных закреплениях. Напомним, что опоры систем (а мы рассматриваем только плоские системы) могут быть следующих типов:
а) Цилиндрическая шарнирная подвижная опора

б) Цилиндрическая шарнирная неподвижная опора

в) Жесткая заделка

Иногда стержни соединяются с помощью шарниров. Различают простые шарниры, когда на одну ось насажены 2 стержня или 2 диска
(диск – кинематически неизменяющаяся часть системы), и кратные
 шарниры, когда на одну ось насажено большее число стержней.
шарниры, когда на одну ось насажено большее число стержней.
Кратный шарнир эквивалентен стольким простым, какова его кратность.  , где
, где 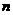 - число стержней (или дисков) в шарнире.
- число стержней (или дисков) в шарнире.
Рама называется статически неопределимой, если внутренние силовые факторы в ней не могут быть определены из условий равновесия.
Иногда различают внешнюю статическую неопределимость, когда из уравнений статики нельзя найти опорные реакции (а, следовательно, и внутренние силовые факторы), и внутреннюю статическую неопределимость, когда реакции опор можно найти из уравнений статики, но внутренние силовые факторы нельзя. Разумеется, что система может быть одновременно статически неопределимой и внешним и внутренним образом. На рис. (а) изображена система стати чески неопределимая внешним образом, а рис.(б) внутренним образом.

Рама, изображенная на рис. (б) или (в), называется замкнутым контуром, легко установить, что замкнутый контур 3 раза статически неопределим (имеет 3 “лишние” связи). На самом деле, разрезав раму, изображенную на рис. (б) или, отбросив одну из опор рамы на рис. в), мы получим статически определимую раму и 3 неизвестных величины.
Для сложной рамы подсчет числа “лишних” неизвестных можно произвести следующим образом. Предположить, что шарниров нет, а все опоры – заделки.

Подсчитать при этих предположениях число неизвестных, а затем учесть, что каждый простой шарнир позволяет составить дополнительное уравнение равновесия, а шарнирные опоры могут быть получены из заделки путем отбрасывания опорных стержней.
 Например, для рамы показанной на рисунке, при высказанных предположениях было бы 3 замкнутых контура, но имеется 3 кратный шарнир и число опорных стержней на 3 единицы меньше чем при заделках. Следовательно, число “лишних” стержней
Например, для рамы показанной на рисунке, при высказанных предположениях было бы 3 замкнутых контура, но имеется 3 кратный шарнир и число опорных стержней на 3 единицы меньше чем при заделках. Следовательно, число “лишних” стержней
 ,
,
В качестве расчетных схем несущих конструкций не могут использоваться так называемые мгновенно изменяемые системы, т.е. системы у которых существует малая подвижность при условии абсолютной жесткости элементов. В подобных системах возникают теоретически бесконечно большие, а практически непомерно большие усилия.
 Примеры:
Примеры:
3 шарнира на одной прямой
Возможно перемещение с практически без удлинений стержней АС и ВС.

Точка А –мгновенный центр вращения. Силу F нельзя уравновесить никакими значениями реакций в точке В.
Метод сил.
Изложение теории будем сопровождать примером расчета рамы. Расчет статически неопределимых систем по методу сил начинается с выбора основной системы.
Определение.
Основной системой называется система статически определимая, кинематически неизменяемая, полученная из данной путем отбрасывания лишних связей.
Замечание 1. Отбрасывание связей осуществляется либо путем отбрасывания опорных стержней, либо путем введения разрезов стержней Замечание 2. Нельзя выбирать в качестве основной системы мгновенно изменяемые системы.
 Согласно аксиоме связей, отбросив связи, мы должны заменить их действия реакциями: реакциями отброшенных опорных закреплений, внутренними силовыми факторами в местах разрезов. Эти реакции отброшенных связей называются обычно основными неизвестными (
Согласно аксиоме связей, отбросив связи, мы должны заменить их действия реакциями: реакциями отброшенных опорных закреплений, внутренними силовыми факторами в местах разрезов. Эти реакции отброшенных связей называются обычно основными неизвестными ( ).
).
Основная система, нагруженная помимо заданных сил основными неизвестными, называется эквивалентной системой. Пример.
Построить эпюру моментов для данной статически неопределимой рамы.
Таким образом, расчет сложной статически неопределимой системы заменяется расчетом более простой статически определимой, но часть нагрузки при этом (основные неизвестные) нам известна. Для того, чтобы найти основные неизвестные надо составить условия эквивалентности исходной системы и основной системы, загруженной помимо заданной нагрузки основными неизвестными. Эти условия обычно записываются в форме канонических уравнений метода сил

где:  матрица единичных перемещений или
матрица единичных перемещений или
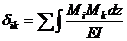 или
или 
 - изгибающие моменты в основной системе соответственно от сил
- изгибающие моменты в основной системе соответственно от сил 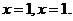
 - соответственно площадь эпюры моментов и ордината под центром тяжести при вычислении интеграла Мора по правилу Верещагина.
- соответственно площадь эпюры моментов и ордината под центром тяжести при вычислении интеграла Мора по правилу Верещагина.
Т.е.  - перемещение по направлению силы
- перемещение по направлению силы 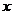 , вызванное силой
, вызванное силой  .
.
По теореме о взаимности перемещений 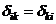 при
при  т.е. матрица
т.е. матрица  симметрична.
симметрична.
Очевидно, что при  . Эти коэффициенты, стоящие на главной диагонали матрицы, называют обычно главными, а остальные – побочными.
. Эти коэффициенты, стоящие на главной диагонали матрицы, называют обычно главными, а остальные – побочными.
 - вектор основных неизвестных;
- вектор основных неизвестных;
 -вектор перемещений в основной системе от заданной силы
-вектор перемещений в основной системе от заданной силы
 или
или 
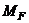 - изгибающий момент от заданной нагрузки.
- изгибающий момент от заданной нагрузки.
Понятно, что 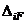 - перемещение по направлению силы
- перемещение по направлению силы  , вызванное заданной нагрузкой.
, вызванное заданной нагрузкой.
Если записать уравнения (1) в обычной форме, то они будут выглядеть 
 (1а)
(1а)
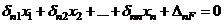
Разберемся в смысле записанных уравнений. Рассмотрим первое из них:
 - перемещение по направлению силы
- перемещение по направлению силы 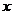 , вызванное ее же самой,
, вызванное ее же самой,
 -перемещение в том же направлении,вызванное силой
-перемещение в том же направлении,вызванное силой 
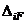 - перемещение в направлении силы
- перемещение в направлении силы 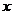 , вызванное заданными силами.
, вызванное заданными силами.
Таким образом, каждое из канонических уравнений метода сил можно трактовать как условие равенства нулю перемещения по направлению отброшенной связи (связь то на самом деле есть и она не допускает перемещений в своем направлении).
Для того, чтобы определить коэффициенты в свободные члены системы (1) надо к основной системе приложить единичные силы по направлению основных неизвестных (прикладывая каждую силу порознь), построить единичные эпюры, затем построить эпюру в основной системе от заданных сил. Перемножая полученные эпюры по правилу Верещагина, находим основные неизвестные. Система канонических уравнений в рассматриваемом примере:

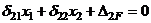
Построим единичные и грузовые эпюры
Перемножим эпюры по правилу Верещагина.
Экстремум эпюры моментов найдем из суммарной эпюры.
ЛЕКЦИЯ XIV
 2018-01-21
2018-01-21 1726
1726
