Работа первой силы на перемещении ее точки приложения, вызванном второй силой равняется работе второй силы на перемещении ее точки приложения, вызванном первой силой.
Будем считать, что система консервативна и работа в ней не зависит от промежуточных состояний, а зависит лишь от начального и конечного состояния системы.
(Линейно-упругие системы всегда консервативны, если загружены консервативными силами, т.е. силами, имеющими потенциал).
 В качестве модели системы выберем консольную балку. Перемещения будем обозначать
В качестве модели системы выберем консольную балку. Перемещения будем обозначать  - перемещение по направлению силы
- перемещение по направлению силы  , вызванное силой
, вызванное силой 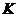 .
.
Нагрузим систему вначале силой  , а затем приложим силу
, а затем приложим силу 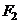 . Работа сил, приложенных к системе запишется:
. Работа сил, приложенных к системе запишется:

(Почему два первых члена имеют множитель 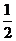 , а последний нет?)
, а последний нет?)
Затем первой приложим силу  а второй -
а второй -  .
.

Т.к. система консервативна, а также потому, что начальные и конечные состояния в обоих случаях совпадают, то работы необходимо равны, откуда следует 
Если положить 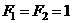 , то получим частный случай теоремы Бетти – теорему о взаимности перемещений.
, то получим частный случай теоремы Бетти – теорему о взаимности перемещений.
Перемещения, вызванные единичными силами, мы будем обозначать  (смысл индексов прежний). Тогда
(смысл индексов прежний). Тогда 
Потенциальная энергия деформации плоской
Стержневой системы.
Будем рассматривать плоскую систему, т.е. систему все стержни которой и все силы лежат в одной плоскости. В стержнях такой системы в общем случае могут возникать при внутренних силовых факторах: 
Упругая система деформируясь накапливает при этом энергию (упругую энергию) называемую потенциальной энергией деформации.
 а) Потенциальная энергия деформации при растяжении и сжатии.
а) Потенциальная энергия деформации при растяжении и сжатии.
Потенциальная энергия накопленная в малом элементе длиной dz будет равняться работе сил приложенных к этому элементу

Потенциальная энергия для стержня: 
Замечание.  и
и  - необязательно постоянные величины.
- необязательно постоянные величины.
б) Потенциальная энергия при изгибе.


Для стержня: 
в) Поперечные силы вызывают сдвиги, и им соответствует по
тенциальная энергия сдвига. Однако, эта энергия в большинстве случаев невелика и мы не будем ее учитывать.
Замечание. В качестве рассматриваемых объектов у нас фигурировали прямые стержни, но полученные результаты применимы и криволинейным стержням малой кривизны, у которых радиус кривизны приблизительно в 5 раз и более превосходит высоту сечения.
Потенциальная энергия для стержневой системы может быть записана: 
Здесь учтено то обстоятельство, что при растяжении и сжатии сечения не поворачиваются, следовательно, изгибающие моменты при этом работы не совершают, а при изгибе не меняется расстояние по оси между смежными сечениями и работа нормальных сил равна нулю. Т.е. потенциальную энергию изгиба и растяжения – сжатия можно вычислить независимо.
Знаки стимулирования означают, что потенциальная энергия вычисляется для всей системы.
Теорема Кастельяно.
Выражение (3) показывает, что потенциальная энергия деформации является однородной квадратичной функцией  и
и  , а те в свою очередь линейно зависят от сил, действующих на систему
, а те в свою очередь линейно зависят от сил, действующих на систему  таким образом
таким образом  является квадратичной функцией сил.
является квадратичной функцией сил.
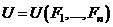
Теорема. Частная производная от потенциальной энергии по силе равняется перемещению точки приложения этой силы по направлению последней.
Доказательство:
Пусть  - потенциальная энергия, соответствующая силам системы
- потенциальная энергия, соответствующая силам системы  Рассмотрим два случая.
Рассмотрим два случая.
1) Вначале приложены все силы  а затем одна из них получает малое приращение
а затем одна из них получает малое приращение  тогда полная потенциальная энергия равна:
тогда полная потенциальная энергия равна: 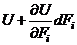
2) Вначале приложена сила  а затем прикладываются силы
а затем прикладываются силы  В этом случае потенциальная энергия равна:
В этом случае потенциальная энергия равна:

Т.к. начальное и конечное состояние в обоих случаях одинаково, а система консервативна, то потенциальные энергии надо приравнять 
Отбрасывая малые второго порядка, получаем 
Интеграл Мора.
Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.
 Пусть задана произвольная стержневая система и нам нужно определить в ней перемещение точки
Пусть задана произвольная стержневая система и нам нужно определить в ней перемещение точки  по направлению
по направлению  , вызванное всеми силами системы -
, вызванное всеми силами системы - 
Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу  , приложенную к точке
, приложенную к точке  и действующую в направлении
и действующую в направлении  . Тогда внутренние силовые факторы в системе можно выразить
. Тогда внутренние силовые факторы в системе можно выразить

 , где
, где  - внутренние силовые факторы в системе от действующих сил;
- внутренние силовые факторы в системе от действующих сил;
 - внутренние силовые факторы от силы
- внутренние силовые факторы от силы 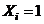 .
.
Внесем эти выражения в (3)

По теореме Кастельяно:
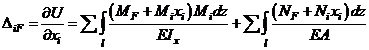
Учтя, что 
получаем выражение: 
называемое интегралом Мора.
Для того, чтобы определить перемещение с помощью метода Мора, необходимо:
1) Определить внутренние силовые факторы в системе от заданных сил.
2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.
3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.
Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит: 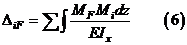
Пример.
ЛЕКЦИЯ XII
 2018-01-21
2018-01-21 2189
2189
