Теорема (Необходимое условие экстремума функции Лагранжа) /Принцип Лагранжа/ Точка Х* является точкой условного экстремума целевой функции Z = f(Х) при заданных уравнениях связи gi(Х) = 0 (1 ≤ i ≤ m), если ранг матрицы, составленной из частных производных 1-го порядка функций ограничений gi(Х) по переменным x1, x2, …,xn, равен m, и существуют числа λ1,…,λm, не равные одновременно нулю.
Математическая модель задачи нелинейного программирования в общем виде формулируется следующим образом: найти вектор 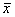 = (х 1, X 2, …, Xn), удовлетворяющий системе ограничений
= (х 1, X 2, …, Xn), удовлетворяющий системе ограничений
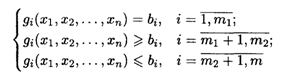
И доставляющий экстремум (наибольшее или наименьшее значение) целевой функции
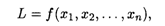
Где Xj — переменные, J = 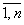 ; L, F, Gi — заданные функции от N переменных, Bi — фиксированные значения.
; L, F, Gi — заданные функции от N переменных, Bi — фиксированные значения.
Нелинейное программирование применяется при прогнозировании промышленного производства, управлении товарными ресурсами, планировании обслуживания и ремонта оборудования и т. д.
Для задачи нелинейного программирования в отличие от линейных задач нет единого метода решения. В зависимости от вида целевой функции и системы ограничений разработаны специальные методы решения, к которым относятся методы множителей Лагранжа, квадратичное и выпуклое программирование, градиентные методы, приближенные методы решения, графический метод.
Из нелинейного программирования наиболее разработаны задачи, в которых система ограничений линейная, а целевая функция нелинейная. Однако даже для таких задач оптимальное решение может быть найдено для определенного класса целевых функций. Например, когда целевая функция сепарабельная, т. е. является суммой П функций Fj(Xj), или квадратичная. При этом следует отметить, что в отличие от задач линейного программирования, где точками экстремума являются вершины многогранника решений, в задачах с нелинейной целевой функцией точки могут находиться внутри многогранника, на его ребре или в вершине.
При решении задач нелинейного программирования для целевой функции необходимо определить глобальный максимум или глобальный минимум. Глобальный максимум (минимум) функции — это ее наибольшее (наименьшее) значение из локальных максимумов (минимумов).
Наличие локальных экстремумов затрудняет решение задач, так как большинство существующих методов нелинейного программирования не позволяет установить, является найденный экстремум локальным или глобальным. Поэтому имеется возможность в качестве оптимального решения принять локальный экстремум, который может существенно отличаться от глобального.
| Графический метод. Задача с линейной целевой функцией и нелинейной системой ограничений | 
|  
|
Рассмотрим примеры решения задач нелинейного программирования с двумя переменными, причем их целевые функции и системы ограничений могут быть заданы в линейном и нелинейном виде. Так же как и в задачах линейного программирования, они могут быть решены графически.
Пример 1. Найти глобальные экстремумы функции
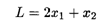 При ограничениях:
При ограничениях:
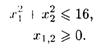 Решение. Область допустимых решений — часть окружности с радиусом 4, которая расположена в первой четверти (рис. 28.1).
Решение. Область допустимых решений — часть окружности с радиусом 4, которая расположена в первой четверти (рис. 28.1).
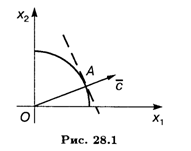 Линиями уровня целевой функции являются параллельные прямые с угловым коэффициентом, равным -2. Глобальный минимум достигается в точке O (0, 0), глобальный максимум — в точке А касания линии уровня и окружности. Проведем через точку А прямую, перпендикулярную линии уровня. Прямая проходит через начало координат, имеет угловой коэффициент 1/2 и уравнение X 2 = 1/2 Х 1.
Решаем систему
Линиями уровня целевой функции являются параллельные прямые с угловым коэффициентом, равным -2. Глобальный минимум достигается в точке O (0, 0), глобальный максимум — в точке А касания линии уровня и окружности. Проведем через точку А прямую, перпендикулярную линии уровня. Прямая проходит через начало координат, имеет угловой коэффициент 1/2 и уравнение X 2 = 1/2 Х 1.
Решаем систему
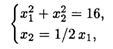 Откуда находим Х 1 = 8
Откуда находим Х 1 = 8 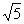 /5, X 2 = 4 /5, X 2 = 4 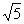 /5, L = 16 /5, L = 16 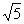 /5 + 4 /5 + 4 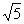 /5 = 4 /5 = 4 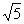 .
Ответ. Глобальный минимум, равный нулю, достигается в точке O (0, 0), глобальный максимум, равный 4 .
Ответ. Глобальный минимум, равный нулю, достигается в точке O (0, 0), глобальный максимум, равный 4 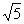 , — в точке А (8 , — в точке А (8 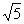 /5, 4 /5, 4 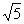 /5). /5).
|
Заключение
Процесс проектирования информационных систем, реализующих новую информационную технологию, непрерывно совершенствуется. В центре внимания инженеров-системотехников оказываются все более сложные системы, что затрудняет использование физических моделей и повышает значимость математических моделей и машинного моделирования систем. Машинное моделирование стало эффективным инструментом исследования и проектирования сложных систем. Актуальность математических моделей непрерывно возрастает из-за их гибкости, адекватности реальным процессам, невысокой стоимости реализации на базе современных ПЭВМ. Все большие возможности предоставляются пользователю, т. е. специалисту по моделированию систем средствами вычислительной техники. Особенно эффективно применение моделирования на ранних этапах проектирования автоматизированных систем, когда цена ошибочных решений наиболее значительна.
Современные вычислительные средства позволили существенно увеличить сложность используемых моделей при изучении систем, появилась возможность построения комбинированных, аналитико-имитационных моделей, учитывающих все многообразие факторов, имеющих место в реальных системах, т. е. использованию моделей, более адекватных исследуемым явлениям.
 2018-01-21
2018-01-21 666
666







