Введем понятие случайного события. Поскольку в дальнейшем будем рассматривать только случайные события, то, начиная с этого момента, будем называть, как правило, просто событиями.
Любой набор элементарных исходов, или, иными словами, произвольное подмножество пространства элементарных исходов, называют событием.
Элементарные исходы, которые являются элементами рассматриваемого подмножества (события), называют элементарными исходами, благоприятствующими данному событию, или образующими это событие.
События будем обозначать прописными латинскими буквами, снабжая их при необходимости индексами, например: А, В 1, С 3 и т.д.
Говорят, что событие А произошло (или наступило), если в результате опыта появился какой-либо из элементарных исходов  .
.
Замечание 1. Для удобства изложения материала термин «событие» как подмножество пространства элементарных событий Ω отождествляется с термином «событие произошло в результате опыта», или «событие заключается в появлении каких-то элементарных исходов».
Так в примере 2, где  , событием А является подмножество
, событием А является подмножество  . Но мы будем также говорить, что событие А – это появление любого из элементарных исходов
. Но мы будем также говорить, что событие А – это появление любого из элементарных исходов 
Пример 1.5. В примере 2 было показано, что при однократном бросании игральной кости
 ,
,
где  - элементарный исход, заключающийся в выпадении i очков. Рассмотрим следующие события: А – выпадение четного числа очков; В - выпадение нечетного числа очков; С – выпадение числа очков, кратного трем. Очевидно, что
- элементарный исход, заключающийся в выпадении i очков. Рассмотрим следующие события: А – выпадение четного числа очков; В - выпадение нечетного числа очков; С – выпадение числа очков, кратного трем. Очевидно, что
 ,
, 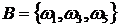 ,
, 
Событие, состоящее из всех элементарных исходов, т.е. событие, которое обязательно происходит в данном опыте, называют достоверным событием.
Достоверное событие обозначают буквой Ω.
Событие  , противоположное достоверному событию Ω, называется невозможным. Очевидно, невозможное событие
, противоположное достоверному событию Ω, называется невозможным. Очевидно, невозможное событие  не может появиться в результате опыта. Например, выпадение более шести очков при бросании игральной кости. Невозможное событие будем обозначать через
не может появиться в результате опыта. Например, выпадение более шести очков при бросании игральной кости. Невозможное событие будем обозначать через  Ø.
Ø.
Невозможное событие не содержит в своем составе ни одного элементарного события. Ему соответствует так называемое «пустое множество», не содержащее ни одной точки.
Геометрически случайные события изображаются множествами точек области Ω, т.е. областями, лежащими внутри Ω (рис. 1.1). Достоверному событию соответствует вся область Ω.
В теории вероятностей над событиями производят различные операции, совокупность которых образует так называемую алгебру событий, тесно связанную с алгеброй логики, широко используемой в современных вычислительных машинах.

Рис. 1.1 Рис. 1.2
Для рассмотрения задач алгебры событий введем основные определения.
Два события называются равносильными (эквивалентными), если они состоят из одних и тех же элементарных событий. Эквивалентность событий обозначается знаком равенства:
А = В.
Событие В называется следствием события А:
А  В,
В,
Если из появления А следует появление В. Очевидно, если А  В и В
В и В  А, то А = В, если А
А, то А = В, если А  В и В
В и В  С, то А
С, то А  С (рис. 1.2).
С (рис. 1.2).
Суммой или объединением двух событий А и В называется такое событие С, которое состоит или в осуществлении события А, или события В, или событий А и В вместе. Условно записывают так:
С = А + В или С = А 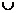 В.
В.
Суммой любого числасобытий А 1, А 2, …, А n называется событие С, которое состоит в осуществлении хотя бы одного из этих событий и записывается в виде
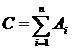 или
или 
Произведением или совмещением (пересечением) двух событий А и В называется событие С, которое состоит и в осуществлении события А, и события В. Условно записывают так:
С = АВ или С = А  В.
В.
Аналогично определяется произведение любого числа событий. Событие С, эквивалентное произведению n событий А 1, А 2, …, А n записывается в виде
 или
или  .
.
Сумма и произведение событий обладают следующими свойствами.
1. А + В = В + А.
2. (А + В)+ С = А +(В + С)= А + В + С.
3. АВ = ВА.
4. (АВ) С = А (ВС)= АВС.
5. А (В + С)= АВ + АС.
Большинство из них легко проверить самостоятельно. Рекомендуем пользоваться при этом геометрической моделью.
Приведем доказательство 5-го свойства.
Событие А (В + С) состоит из элементарных событий, которые принадлежат и А и В + С, т.е. событию А и хотя бы одному из событий В, С. Иначе говоря, А (В + С) – это множество элементарных событий, принадлежащих либо событию АВ, либо событию АС, т.е. событию АВ + АС. Геометрически событие А (В + С) представляет собой общую часть областей А и В + С (рис. 1.3.а), а событие АВ + АС – объединение областей АВ и АС (рис. 1.3.б), т.е. ту же самую область А (В + С).

Рис. 1.3.а Рис. 1.3.б
Событие С, состоящее в том, что событие А происходит, а событие В не происходит, называется разностью событий А и В. Условно записывают так:
С = А - В.
События А и В называются совместными, если они могут появиться в одном и том же испытании. Это значит, что существуют такие элементарные события, которые входят в состав и А и В одновременно (рис. 1.4).
События А и В называются несовместными, если появление одного из них исключает появление другого, т.е. если АВ = Ø. Иными словами, нет ни одного элементарного события, которое входило бы в состав и А и В одновременно (рис. 1.5). В частности, противоположные события 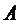 и
и  всегда несовместны.
всегда несовместны.

Рис. 1.4 Рис. 1.5
События  называются попарно несовместными, если любые два из них несовместны.
называются попарно несовместными, если любые два из них несовместны.
События  образуют полную группу, если они попарно несовместны и в сумме дают достоверное событие, т.е. если для любых i, k
образуют полную группу, если они попарно несовместны и в сумме дают достоверное событие, т.е. если для любых i, k
 Ø;
Ø;  .
.
Очевидно, каждое элементарное событие должно входить в состав одного и только одного события полной группы  . Геометрически это значит, что вся область Ω области
. Геометрически это значит, что вся область Ω области  делят на n частей, не имеющих между собой общих точек (рис. 1.6).
делят на n частей, не имеющих между собой общих точек (рис. 1.6).

Рис. 1.6
Противоположные события 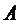 и
и  представляют собой простейший случай полной группы.
представляют собой простейший случай полной группы.
 2018-01-21
2018-01-21 1657
1657








