СЛУЧАИ СИММЕТРИИ


Рисунок 4.3. Функция, симметричная относительно оси ординат.





Рисунок 4.4. Функция, симметричная относительно начала координат.

Рисунок 4.5. Функция, симметричная относительно оси абсцисс при совмещении двух полупериодов во времени.


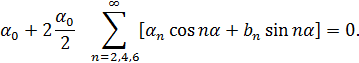
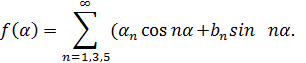
f(α) = - f(π - α).
п cos nα = = - cos п (π - α),

f(α) = - f(π - α),
п sin п а = sin п (π - α):

Таблица 4.1
Условия симметрии и коэффициенты ряда Фурье
| № П/п | Симметрия относительно | Математическое условие | Коэффициенты | ||
| Оси ординат (четная функция) Оси ординат (четная функция) Оси абцисс при совмещении 2х полупериодов Случаи 1 и 3 одновременно Случаи 2 и 3 одновременно | 


 = = 

| Есть Нули Нуль Нули Нули | Есть Нули Есть только нечетные Есть только нечетные Нуль | Нули Есть Есть только нечетные Нуль Есть только нечетные |
ПЕРЕНОС НАЧАЛА ОТСЧЕТА


КОМПЛЕКСНАЯ ФОРМА РЯДА ФУРЬЕ







 (4.12)
(4.12)
 (4.12)
(4.12)

Рисунок 4.9. Синусоидальная функция как сумма двух сопряженных векторов, вращающихся в противоположных направлениях,
ПРИМЕНЕНИЕ РЯДА ФУРЬЕ К РАСЧЕТУ ПЕРИОДИЧЕСКОГО НЕСИНУСОИДАЛЬНОГО ПРОЦЕССА

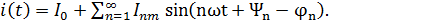 (4.14)
(4.14)
где


 .
.
ап = nωt = па,


Где


Рисунок 4.10. Соотношение масштабов углов для разных гармоник
ДЕЙСТВУЮЩЕЕ И СРЕДНЕЕ ЗНАЧЕНИЯ ПЕРИОДИЧЕСКОЙ НЕСИНУСОИДАЛЬНОЙ ФУНКЦИИ





МОЩНОСТЬ В ЦЕПИ ПЕРИОДИЧЕСКОГО НЕСИНУСОИДАЛЬНОГО ТОКА

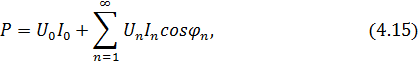

КОЭФФИЦИЕНТЫ, ХАРАКТЕРИЗУЮЩИЕ ПЕРИОДИЧЕСКИЕ НЕСИНУСОИДАЛЬНЫЕ ФУНКЦИИ
 (4.16)
(4.16)



kИ = I1/I < 1



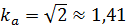
arccosχ,
ВЫСШИЕ ГАРМОНИКИ В ТРЕХФАЗНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

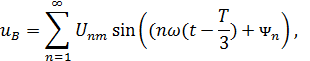

 .
.

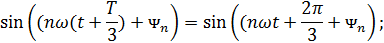








 2018-01-21
2018-01-21 303
303






