МАТЕМАТИКА ДЛЯ ЕКОНОМІСТІВ (169 ГРУПА)
ІНДИВІДУАЛЬНЕ ЗАВДАННЯ №4
ВЕКТОРИ
(Ключ до завдань:
номера прикладів для виконання визначаються в залежності від порядкового номера в списку групи)
Завдання. В задачах 1.1-1.16 задані координати вершин піраміди ABCD в прямокутній декартовій системі координат. Знайти:
1) координати векторів 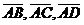 і обчислити довжини цих векторів;
і обчислити довжини цих векторів;
2) кут між векторами 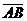 та
та 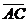 в радіанах;
в радіанах;
3) проекцію вектора 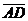 на вектор
на вектор 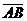 ;
;
4) площу грані АВС;
5) об`єм піраміди ABCD та її висоту DН;
6) кут нахилу бічного ребра АD до площини основи (АВС);
7) кут нахилу бічної грані (АDС) до площини основи (АВС).
Всі обчислення виконати з точністю до двох десяткових знаків.
1.1 А(-4;6;1) В(1;4;1) С(2;2;-3) D(0;4;3)
1.2 A(1;7;-3) В(4;2;4) С(-3;-1;0) D(-1;2;-1)
1.3 A(8;-1;3) В(3;1;3) С(-4;0;5) D(0;2;3)
1.4 A(-5;7;2) В(-2;1;0) С(1;-3;0) D(-2;1;3)
1.5 A(2;6;-1) В(3;2;-3) С(-4;0;0) D(1;0;2)
1.6 A(0;-1;-4) В(6;-3;2) С(2;0;-1) D(2;0;3)
1.7 A(2;-2;-4) В(0;1;4) С(3;-3;1) D(-5;4;7)
1.8 A(9;3;-6) В(0;3;-5) С(-4;5;1) D(7;-3;8)
1.9 A(-7;4;1) В(-2;1;3) С(0;-2;1) D(5;-1;-1)
1.10 A(-2;2;-1) В(4;0;3) С(-3;6;1) D(6;-3;7)
1.11 A(5;-1;7) В(-3;-2;0) С(-3;0;-5) D(6;2;3)
1.12 A(-4;4;-1) В(0;4;1) С(-1;5;3) D(-1;-2;1)
1.13 A(5;-2;7) В(-4;2;0) С(-1;5;5) D(2;-1;8)
1.14 A(8;-6;1) В(0;-5;-1) С(-4;3;1) D(-5;7;-2)
1.15 A(4;-3;1) В(-4;6;0) С(-2;2;1) D(9;-1;-2)
1.16 A(-5;1;-3) В(-4;0;3) С(-1;2;2) D(1;-1;1)
Методичні вказівки до завдання.
Розв’язання задачі.
Дано координати вершин піраміди: 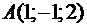 ,
, 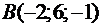 ,
, 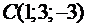 ,
, 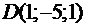 .
.
Побудуємо схематичний малюнок піраміди, не прив’язуючись до системи координат  .
.

1. Довільний вектор 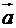 можна записати в системі орт
можна записати в системі орт 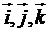 за слідуючою формулою:
за слідуючою формулою: 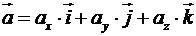 (1)
(1)
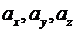 - проекції вектора
- проекції вектора 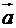 на координатні осі
на координатні осі 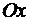 ,
, 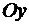 та
та 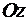 ;
; 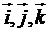 - одиничні вектори, які направлені так, як направлені осі
- одиничні вектори, які направлені так, як направлені осі 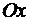 ,
, 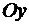 та
та 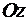 . Якщо задані точки
. Якщо задані точки 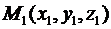 та
та 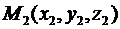 , то проекції вектора
, то проекції вектора 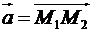 на координатні осі знаходяться за формулами:
на координатні осі знаходяться за формулами:
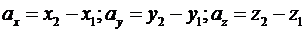 (2)
(2)
Тоді:
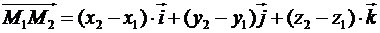 (3)
(3)
Підставляючи в (3) координати точок 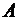 та
та 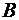 , одержимо вектор
, одержимо вектор 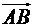 :
:
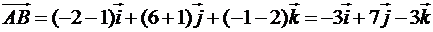 .
.
Аналогічно, підставляючи в (3) координати точок 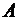 та
та 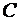 , знаходимо вектор
, знаходимо вектор 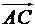 :
:
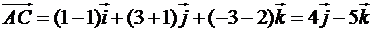 .
.
Підставляючи в (3) координати точок 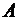 та
та  , одержимо вектор
, одержимо вектор 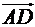 :
:
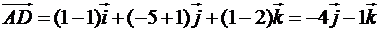 .
.
Отже знайдені вектори 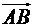 ,
, 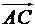 ,
, 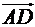 мають такі координати:
мають такі координати:
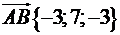
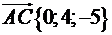
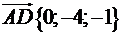 .
.
Якщо вектор 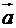 задано формулою (1), або (3), то його модуль (довжина) обчислюється за формулою:
задано формулою (1), або (3), то його модуль (довжина) обчислюється за формулою:
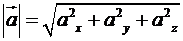
Застосовуючи цю формулу, обчислюємо модулі знайдених векторів 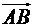 ,
, 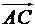 ,
, 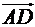 :
:
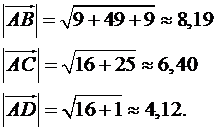
2. Так як скалярний добуток двох векторів 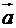 ,
, 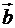 дорівнює добутку їх довжин, помноженому на косинус кута мім ними, тобто:
дорівнює добутку їх довжин, помноженому на косинус кута мім ними, тобто:
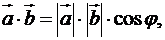 то косинус кута
то косинус кута 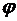 між двома векторами
між двома векторами 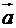 ,
, 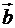 дорівнює скалярному добутку цих векторів, поділеному на добуток їх модулів:
дорівнює скалярному добутку цих векторів, поділеному на добуток їх модулів:
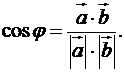 (4)
(4)
Якщо координати векторів-співмножників відомі 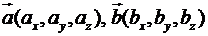 , то їх скалярний добуток можна знайти за формулою:
, то їх скалярний добуток можна знайти за формулою:
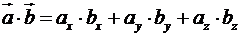 (5)
(5)
Знаходимо скалярний добуток векторів 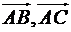 за формулою (5):
за формулою (5):
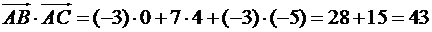
Отже за формулою (4) дістанемо:
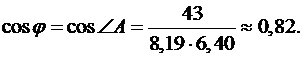
3. Проекція вектора 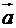 на
на 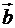 знаходиться за формулою:
знаходиться за формулою:
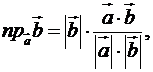 звідки
звідки 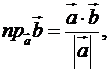
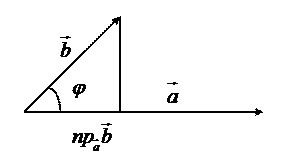
Отже проекція вектора 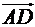 на
на 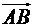 дорівнює скалярному добутку цих векторів, поділеному на модуль вектора
дорівнює скалярному добутку цих векторів, поділеному на модуль вектора 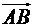 :
:
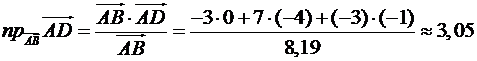 (лін. од.)
(лін. од.)
4. Площа грані 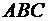 дорівнює половині площі паралелограма, побудованого на векторах
дорівнює половині площі паралелограма, побудованого на векторах 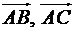 . Позначимо векторний добуток вектора
. Позначимо векторний добуток вектора 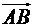 на вектор
на вектор 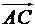 через вектор
через вектор 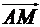 :
:
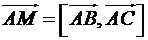 .
.
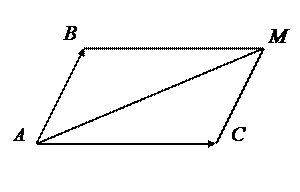
Тоді, виходячи з геометричного змісту модуля векторного добутку двох векторів, величина модуля вектора 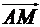 чисельно дорівнює площі паралелограма, побудованого на векторах
чисельно дорівнює площі паралелограма, побудованого на векторах 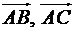 , а площа грані
, а площа грані 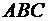 буде чисельно дорівнювати половині модуля вектора
буде чисельно дорівнювати половині модуля вектора 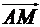 :
:
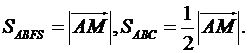
Знайдемо векторний добуток векторів 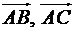 :
:
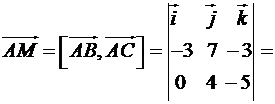
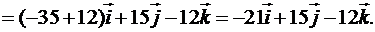
Таким чином, 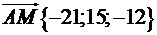 , а його модуль дорівнює:
, а його модуль дорівнює:
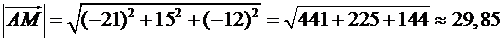 .
.
Отже 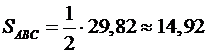 (кв. од.)
(кв. од.)
5. Об`єм паралелепіпеда, побудованого на трьох некомпланарних векторах чисельно дорівнює абсолютній величині їх мішаного добутку:
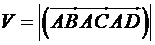 .
.
А об`єм піраміди дорівнює шостій частині від об`єму паралелепіпеда: 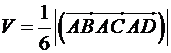 .
.
Обчислимо мішаний добуток:
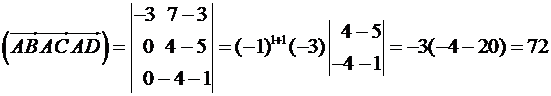
Отже 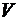 паралелепіпеда дорівнює
паралелепіпеда дорівнює 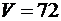 куб. од., а об’єм піраміди
куб. од., а об’єм піраміди 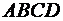
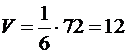 (куб. од.).
(куб. од.).
Тепер можна знайти висоту 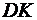 піраміди
піраміди 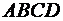 :
:
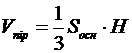 , звідки
, звідки 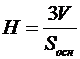 , тому
, тому 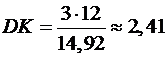 (лін. од.).
(лін. од.).
Отже висота 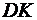 заданої піраміди дорівнює
заданої піраміди дорівнює 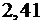 лін. одиниць.
лін. одиниць.
6. Знайдемо кут 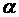 нахилу бічного ребра
нахилу бічного ребра 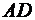 до площини основи
до площини основи 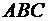 .
.
З трикутника 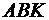 :
: 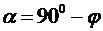 , тому
, тому 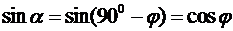 .
.
Кут 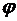 - це кут між векторами
- це кут між векторами 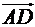 і вектором
і вектором 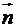 , перпендикулярним до площини основи:
, перпендикулярним до площини основи: 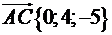 ,
, 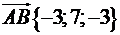 .
.
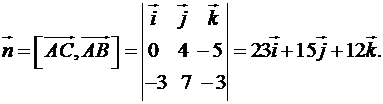 ;
; 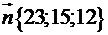 .
.
Знайдемо координати вектора 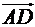 :
: 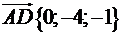 .
.
Тоді
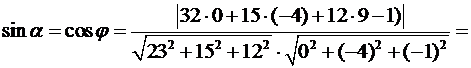
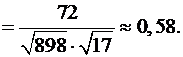
7. Кут 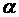 нахилу площини бічної грані
нахилу площини бічної грані 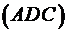 до площини основи
до площини основи 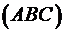 буде дорівнювати куту між векторами
буде дорівнювати куту між векторами 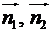 , що відповідно перпендикулярні до цих площин.
, що відповідно перпендикулярні до цих площин.
Для знаходження вектора 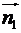 , в площині
, в площині 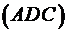 знайдемо координати двох векторів, що лежать в цій площині:
знайдемо координати двох векторів, що лежать в цій площині:
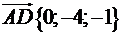 ,
, 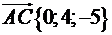 .
.
Тоді 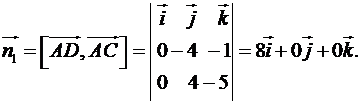 Тобто
Тобто 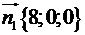 .
.
Аналогічно, 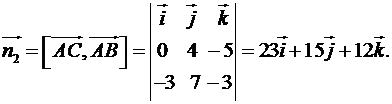
Значить, 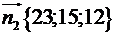 .
.
Тоді за формулою 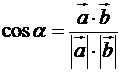 , маємо:
, маємо:
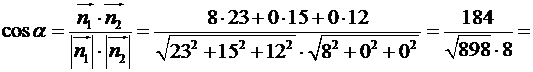
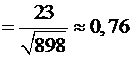 .
.
 2018-01-21
2018-01-21 334
334






