2018-01-21
4226
| Базовые значения | Импликация: | Импликация: | Эквивалентность | Исключающее “или”: | |
| A | B | A -> B | B->A | A ~ B | A  B
|
Пример: таблица истинности выражения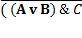 
)
| A | B | C | A v B | (A v B) & C |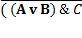
|
Пример вычисления значения выражения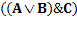 
при заданных значениях логических переменных A = 1, B = 0, C = 1: Вычисляем значение выражения, стоящего под знаком инверсии (A 
B)&C, для этого сначала выполняем операцию в скобках (A B), подставляя значения переменных A и В. По определению дизъюнкции 1 v 0 = 1. Вычислим 1& C = 1, по определениюконъюнкции 1&1 = 1.Итак, (A B)&C) при заданных значениях логических переменных равно 1. Применив инверсию (отрицание), получаем, что при A = 1, B = 0, C = 1 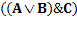= 0.
Преобразование выражений.
|
|
|
Дополнительные операции можно выразить через основные следующим образом:
А 
В = 
vВ;
A ~ B = ( vВ)& (А v 
)= (А&В v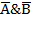 
); (10)
A B =( &В)v (А& );
Знак = означает равносильность.
Два логических выражения равносильны, если их таблицы истинности совпадают с точностью до порядка строк. В равносильности указанных выражений можно убедиться, выписав таблицы истинности для выражений, стоящих справа от знака равносильности, и сравнив их с таблицами истинности для выражений слева
Законы логики и упрощение логических выражений
Подобно алгебре чисел, алгебра логики имеет свои законы, записываемые формулами. Эти законы выражают свойствалогических операций и используются при вычислении значений логических выражений. Упростить – это значит привести выражение к наименьшему количеству основных логических операций: “ИЛИ” (дизъюнкция), “И” (конъюнкция) и “НЕ” (инверсия). Переместительный (коммутативность), распределительный (дистрибутивность), сочетательный (ассоциативность) и некоторые другиезаконы справедливы для операций логического отрицания, сложения и умножения.
Поглощение:
Аv1 = 1, Av0 =A
A&1 = A, А&0 =0
АvA&B =A, A&(AvB) =A
Переместительный закон:
AvB= BvA
A&B= B&A
Сочетательныйзакон:
(AvB) vC= Av (BvC)
(A & B) & C = A & (B & C)
Распределительный закон:
Av (B&C) = (AvB) & (AvC)
A & (B v C) = (A & B) v (A & C)
Закон НЕпротиворечия:
A & 
= 0Этот закон выражает тот факт, что высказывание не может быть одновременно истинным и ложным.
Закон исключенного третьего:
A v = 1Этот закон означает, что либо высказывание, либо его отрицание должно быть истинным.
Закон двойного отрицания:
|
|
|
=A
Законы де Моргана:
= & 
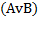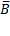
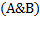= v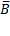
В справедливости указанных законов можно убедиться с помощью таблиц истинности.
Пример использования законов логики при упрощении логического выражения.
Упроститьвыражение A&Bv(
Av B).
Применим закон де Моргана к выражению в скобках ( A v B) = (A&B).
Перепишем исходное выражение, заменив одинаковые выражения (A & B) на С:
A&B v ( A v B) = (A&B) v (A&B) = C v C = И
Итак, данное выражение A&Bv( Av B) всегда имеет значение “истина”, независимо от значений входящих в него переменных. Такие выражения называются тождественноистинными. Если выражение принимает значение “ложь” при любых значениях входящих в него переменных, то оно называется тождественноложным.
Пример. Упростим выражение: (AvC)&(ØAvC)&(BvØC)
Используя распределительный закон, преобразуем конъюнкцию двух первых выраженийв скобках:
1. (AvC)&(ØAvC) =Cv(A&ØA)=CvЛ=C;
Затем преобразуем конъюнкцию полученного результата и последнего выражения в скобках:
2. C&(BvØC)= C&BvC&ØC = C&BvЛ = С&B.
Полученный результат: (AvC)&(ØAvC)&(BvØC) = С&B.
Проверим, построив таблицу истинности для выражений (AvC)&(ØAvC)&(BvØC) и С&B, не нарушая принятого порядка действий для логических операций:
| А | B | C | ØA | ØС | AvC | ØAvC | (AvC)&(ØAvC) | BvØC | (AvC)&(ØAvC)&(BvØC) | С&B. |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| * | * |
Значения столбцов, отмеченных * совпадают, значит, выражения
(AvC)&(ØAvC)&(BvØC) и С&B тождественно равны.
Логические схемы
Логические схемы являются графическим представлением логических выражений. Они конструируются из логических элементов и соединяющих их линий. Логические элементы обозначаются прямоугольниками и соответствуют логическим операциям, линии – частям выражения (в том числе логическим переменным) над которыми эти операции выполняются. Стрелки на концах линий указывают порядок выполнения операций. Переменным, входящим в состав выражения, соответствуют линии-входы. Значению выражения соответствует линия-выход. Иногда на выходе схемы бывает нужно узнать не только значение выражения, но и значения его отдельных частей. В таких случаях у схемы бывает несколько линий-выходов.
Конъюнктор Инвертор Дизъюнктор
| С |
| & |
| А |
| А |
| А |
| В |
| В |
| С== |
| С |
С= А&B C= A C=AvB
Сумматор – это электронная логическая схема,выполняющая суммирование двоичных чисел, он служит центральным узлом арифметико-логического устройства процессоров. Многоразрядный двоичный сумматор представляет собой комбинацию одноразрядных сумматоров.
Триггер – устройство памяти компьютера для хранения одного бита информации. Несколько триггеров можно объединить в группы – регистры (устройства компьютера длякратковременного хранения двоичной информации, для обработки информации).
Регистры памяти – один регистр образует одну ячейку памяти, которая имеет свой адрес и может запомнить столько бит информации, сколько триггеров в неё входит.
Регистр устройства управления (УУ) процессора - счётчик команд – хранит адрес выполняемой в данный моменткоманды, по которому она находится в оперативной памяти. После выполнения данной команды УУ увеличивает значение этого регистра на единицу, т.е. вычисляет адрес в оперативной памяти, по которому расположена следующая команда.
Регистр команд – регистр УУ, служит для вычисления адреса ячейки, где хранятся данные, требуемые выполняемой в данный момент программе.
|
|
|
Регистр флагов – регистр УУ, хранит информацию о последней команде, выполненной процессором.
Контрольные задания даны в 15 вариантах. Номер варианта определяется по списку группы, варианты для номера списка более 15 начинаются заново, с 1.Работы рекомендуется выполнять в печатном или письменном виде, соблюдая методические рекомендации по выполнению контрольных работ.
Рекомендации по выполнению контрольной работы.
Для студентов заочной формы обучения контрольная работа является основной формой межсессионного контроля студенческих знаний. Более того, студент, не выполнивший и не сдавший своевременно на проверку преподавателю контрольную или курсовую работу, не может быть допущен к сдаче зачета (экзамена) по соответствующей дисциплине.
Контрольная работа является одной из форм самостоятельного изучения заочниками программного материала и выполняется по всем дисциплинам. Это своеобразный письменный экзамен, требующий серьезной подготовки. Эта работа способствует расширению и углублению знаний обучающихся.
Однако главное достоинство контрольных работ заключается в том, что при их выполнении студент овладевает навыками работы с научной и учебной литературой, усваивает технику оформления студенческих научных работ, что является крайне важным фактором при подготовке к написанию курсовых и дипломных работ, к которым применяются гораздо более серьезные требования.
Все, что относится к оформлению работ, должно быть сделано в соответствии с изложенными ниже указаниями и обязательно по отношению ко всем контрольным работам студентов заочного отделения.
