Умножение матрицы на число

Лекция№1

МАТРИЦЫ

 

Определение и виды матриц

 

Определение 1.1. Матрицей размера т п называется прямоугольная таблица чисел (или других объектов), содержащая m строк и n столбцов.

Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С,... Числа (или другие объекты), составляющие матрицу, называются элементами матрицы. Элементами матрицы могут быть функции. Для обозначения элементов матрицы используются строчные буквы латинского алфавита с двойной индексацией: аij, где первый индекс i (читается – и) – номер строки, второй индекс j (читается – жи) – номер столбца.

Определение 1.2. Матрица называется квадратной п- го порядка, если число её строк равно числу столбцов и равно одному и тому же числу п

Для квадратной матрицы вводятся понятия главной и побочной диагонали.

Определение 1.3. Главная диагональ квадратной матрицы состоит из элементов, имеющих одинаковые индексы, т. е.. Это элементы: a 11 ,a_22,…

Определение 1.4. Квадратная матрица называется диагональной, если все элементы, кроме элементов главной диагонали, равны нулю

Определение 1.5. Квадратная матрица называется треугольной, если все её элементы, расположенные ниже (или выше) главной диагонали, равны нулю.

Определение 1.6. Квадратная матрица п- го порядка, у которой все элементы главной диагонали равны единице, а остальные равны нулю, называется единичной матрицей n -го порядка, и она обозначается буквой Е.

Определение 1.7. Матрица любого размера называется нулевой, или нуль-матрицей, если все её элементы равны нулю.

Определение 1.8. Матрица, состоящая из одной строки, называется матрицей-строкой.

Определение 1.9. Матрица, состоящая из одного столбца, называется матрицей-столбцом.

А = (а 11 а 12 ... а 1 n) – матрица-строка;

 

Определение 1.10. Две матрицы А и В одинаковых размеров называ- ются равными, если равны между собой все соответствующие элементы этих матриц, т. е. aij = bij для любых i = 1, 2,..., т; j = 1, 2,…, n.

 

Операции над матрицами

Над матрицами, как и над числами, можно производить ряд операций. Основными операциями над матрицами являются сложение (вычитание) матриц, умножение матрицы на число, умножение матриц. Эти операции аналогичны операциям над числами. Специфическая операция – транспонирование матрицы.

 

Умножение матрицы на число

 

Определение 1.11. Произведением матрицы А на число λ называется матрица В = А, элементы которой получены умножением элементов мат рицы А на число λ.

Пример 1.1. Найти произведение матрицы А= 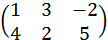на число 5.

Решение. ►.◄ 5A=

Правило умножения матрицы на число: чтобы умножить матрицу на число, надо умножить на это число все элементы матрицы.

Следствие.

1. Общий множитель всех элементов матрицы можно вынести за знак матрицы.

 

2. Произведение матрицы А на число 0 есть нулевая матрица: А · 0 = 0.

 

Сложение матриц

 

Определение 1.12. Суммой двух матриц А и В одинакового размера т n называется матрица С = А + В, элементы которой получены путём сложения соответствующих элементов матрицы А и матрицы В, т. е. cij = aij + bij для i = 1, 2,..., m; j = 1, 2,..., n (т. е. матрицы складываются поэлементно).

Следствие. Сумма матрицы А с нулевой матрицей равна исходной матрице: А + О = А.

1.2.3. Вычитание матриц

Разность двух матриц одинакового размера определяется через пре- дыдущие операции: А – В = А + (– 1 )В.

Определение 1.13. Матрица –А = (– 1 )А называется противоположной матрице А.

Следствие. Сумма противоположных матриц равна нулевой матрице: А + (–А) = О.

 

Умножение матриц

 

Определение 1.14. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй матрицы. Тогда произведением матриц называется такая матрица, каждый элемент которой cij равен сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы B.

 

Пример 1.4. Вычислить произведение матриц А · В, где

A=

A*B=

 

=

 

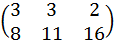
Пример 1.5. Найти произведения матриц АВ и ВА, где

A= , B=

 

AB= , BA=

 

Замечания. Из примеров 1.4–1.5 следует, что операция умножения матриц имеет некоторые отличия от умножения чисел:

1) если произведение матриц АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать. Действительно, в примере 1.4 произведение матриц AB существует, а произведение ВА не существует;

2) если даже произведения АВ и ВА существуют, то результат произведения может быть матрицами разного размера. В случае, когда оба произведения АВ и ВА существуют и оба – матрицы одинакового размера (это возможно только при умножении квадратных матриц одного порядка), то коммутативный (переместительный) закон умножения всё равно не выполняется, т.е. А В В А, как в примере 1.5;

3) однако если перемножить квадратную матрицу А на единичную матрицу Е того же порядка, тогда АЕ = ЕА = А.

Таким образом, единичная матрица при умножении матриц играет ту же роль, что и число 1 при умножении чисел;

4) произведение двух ненулевых матриц может равняться нулевой матрице, т. е. из того, что А В = 0, не следует, что А = 0 или B = 0.