Пример 1
Постановка задачи
Факторная система определена следующими зависимостями:
А=(В1+В2)*[f1*c1+f2*c2]; B=B1+B2; A=A1+A2; A=B*c; c=∑fi*ci
Исходная информация:
| Показатели | База | Отчет | Рост, % |
| В1 | 130,0 | ||
| В2 | 84,0 | ||
| А1 | 125,0 | ||
| А2 | 112,0 |
Определить:
1.Абсолютное отклонение результативного показателя А от влияния факторов с1, f2;
2.Относительное отклонение результативного показателя А от влияния каждого из факторов: В, f1, с.
Выполнить аналитические проверки полученных результатов.
Формализация задачи
| А |
| В |
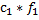 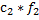 |
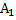 |
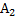 |
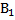 |
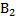 |
 |
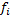 |
Пояснение
Результативный показатель в данной факторной системе выражен в простой прямой мультипликативной связи. Но в факторной системе присутствуют также аддитивные связи, и есть наличие структурного коэффициента.
При решении этой задачи способ долевого распределения (участия) не может быть применён, исходя из условия задачи. В данной модели нет субфактора, находящегося в обратной взаимосвязи с результативным показателем (это является основным условием применения способа долевого распределения).
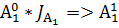
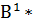 Δ
Δ 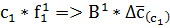
При нахождении относительного изменения мы можем использовать способ относительных величин и с помощью 3-компонентной формулы.
Решение
Дана многофакторная (сложная) аддитивно-мультипликативная модель
А = (В1+В2)*(f1*c1 + f2*c2)
Критерии ранжирования, использованные при решении задачи:
1. Количественные факторы анализируются раньше качественных;
2. В сложной функциональной зависимости, выраженной формулой средней арифметической структурные коэффициенты анализируются раньше качественных признаков.
3. При аддитивной зависимости факторы-слагаемые анализируются одновременно.
Информационная база представлена в неполном объеме, а дополнительные данные при необходимости можно определить по расчетным формулам.
Цель анализа: абсолютное отклонение результативного показателя (РП) А от влияния факторов c1,f2; относительное отклонение РП А от влияния каждого из факторов В, f1, с.
| Стр. изм. |
| Стр. изм. |
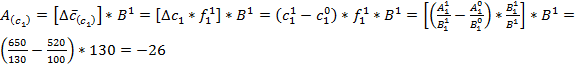
±Δ 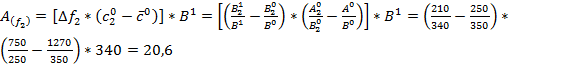
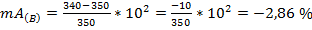
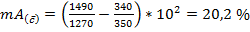
±Δ 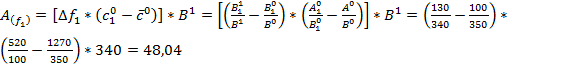
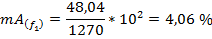
Пример 2
Некоторая производственная ситуация выражена взаимосвязанной системой показателей в виде их функциональных зависимостей:
X= Б/Д; Б = А+В; Д = Е-F,
причем фактор Б отражает результат деятельности, а фактор Д - условия производства.
ИСХОДНАЯ ИНФОРМАЦИЯ:
| Показатели | План | Фактически |
| А | ||
| В | ||
| Е | ||
| F | ||
| X | 5,0 | 4,0 |
ОПРЕДЕЛИТЬ:
1) Абсолютные величины изменений результативного показателя X от влияния факторов В и F;
2) Относительные его изменения от влияния факторов Е, Д.
3) Найти долю влияния в общей величине изменения результативного показателя факторов, характеризующих условия производства.
Примечание: Необходимую для анализа информацию можно рассчитать дополнительно.
Решение:
В сложной многофакторной системе – факторы, отражающие условия производства, ранжируются ранее факторов – результата деятельности.
При аддитивной зависимости факторы – слагаемые анализируются одновременно.
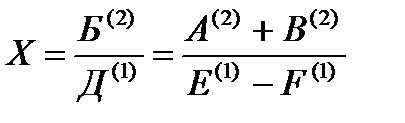
Даны все первичные показатели на плановом и фактическом уровнях (абсолютные величины), так же дан результативный показатель в обоих периодах.
Схема взаимосвязей параметров анализируемой системы:
X
Б2 Д1
А2 B2 E1 F1
Каналы взаимосвязи (путь следования от первичных факторов до результативного показателя):
B 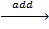 Б
Б 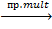 X;
X;
Б= А+В Х= 
F 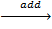 Д
Д 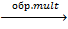 X;
X;
Д= E- F Х= 
E 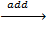 Д
Д 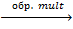 X;
X;
Д= E- F Х= 
Д 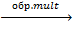 X
X
Х= 
Способ цепных подстановок:
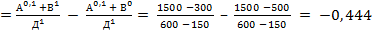 ;
;
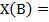 Способ разниц:
Способ разниц:
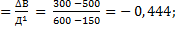
Способ корректировок не применим:
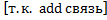 .
.
Для обратной аддитивной зависимости обязательно использование способа долевого распределения отклонений (способ долевого участия):
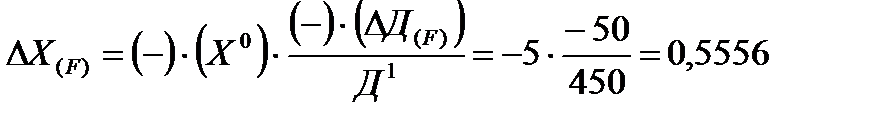
Используя для вычислений исходную базу данных целесообразней воспользоваться трехкомпонентной формулой:
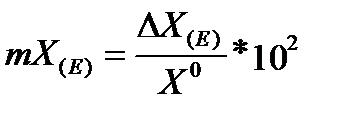
Далее вновь используется способ долевого распределения отклонений (способ долевого участия), т.к. зависимость обратная аддитивная:
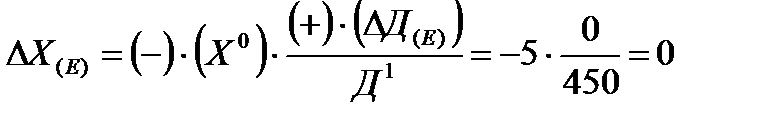 , т.о.
, т.о. 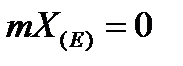
Используем трехкомпонентную формулу:
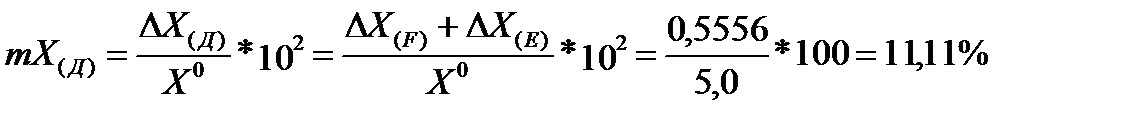
Проверка: получение результата другим способом (относительных величин):
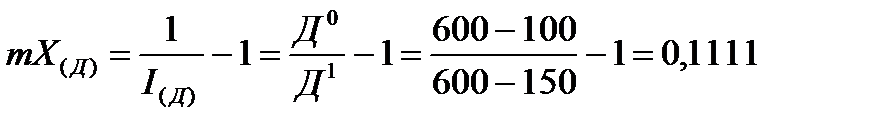
ОТВЕТ:
| Изменение Х | От влияния факторов: | |||
| В | F | E | Д | |
| Абсолютное | - 0,444 | 0, 556 | ||
| Относительное | 0 | 11,12% |
Пример 3.
Дана многофакторная (сложная) аддитивно-мультипликативная модель Х = 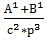 ; M = K/c; K = A+B; X = M/p,
; M = K/c; K = A+B; X = M/p,
где: X- результативный показатель;
с, р - качественные факторы;
остальные факторы - количественные.
Исходные данные:
| Показатели | План | Отчет | Выполнение, % |
| A | 120,0 | ||
| K | 120,0 | ||
| p | - | - | 95,3 |
| X | 24,0 | 25,0 | 104,2 |
Критерии ранжирования, используемые при решении задачи:
1. Количественные факторы анализируются раньше качественных;
2. При наличии в формуле нескольких качественных факторов качественный фактор первого уровня детализации анализируется в последнюю очередь среди качественных; качественный фактор последнего уровня детализации анализируется в первую очередь среди качественных; в модели субфакторы являются количественными.
3. При аддитивной зависимости факторы-слагаемые анализируются одновременно.
Число первичных факторов n =4 (А, В, с, р), входящих в аналитическую формулу расчета результативного показателя (РП);
Число параметров факторной системы: (n+1) =4+1=5 (А, В, с, р, Х);
Количество этапов детализации n-1 =4-1=3 этапа.
Информационная база представлена не в полном объеме, дана полная информация только по факторам А, К и Х. А также процент выполнения по качественному фактору р.
Цель анализа: абсолютное изменение РП Х от влияния факторов А и с;
относительное изменение РП Х от влияния фактора р;
изменение РП Х от влияния роста фактора А на 2,5%.
±∆Х(А) Первичный фактор А находится в прямой аддитивной зависимости с РП Х. На данном этапе элиминирования можно использовать следующие способы: цепных подстановок, разниц, относительных величин (ОВ).
| Х |
| М |
| К |
| А1 |
| с2 |
| р3 |
| В1 |
| mult |
| mult |
| add |
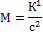 |
| К=А+В |
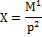 |
| mult |
| обр. mult |
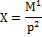 |
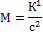 |
| обр. mult |
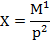 |
 2017-11-01
2017-11-01 989
989








