Погрешность измерения величин

Лабораторная работа №3. Погрешность функции.

Общая постановка задачи

Основной целью выполнения лабораторной работы является ознакомление с основами работы с погрешностями в среде MatLAB.

В ходе работы необходимо рассчитать погрешности согласно задания.

 

Теоретическая часть

Погрешность измерения величин

Пусть x – приближённое значение некоторой величины (например, полученное путём однократного измерения этой величины), а x₀ – её точное значение.

Абсолютной погрешностью величины называется разность Δ x = | x – x ₀|.

Пример. В школе 1254 учащихся. При округлении этого числа до 1200 абсолютная погрешность составляет Δ = |1200 – 1254| = 54, а при округлении до 1250: Δ = |1250 – 1254| = 4.

Относительной погрешностью приближённого числа называется отношение абсолютной погрешности приближённого числа к самому этому числу:

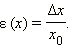
Пример 1.

В школе 1254 учащихся. При округлении этого числа до 1200 абсолютная погрешность составляет

Δ = |1200 – 1254| = 54, относительная погрешность равна 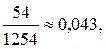или 4,3 %.

При округлении до 1250: Δ = |1250 – 1254| = 4, а относительная погрешность 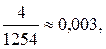или 0,3 %.

В научных экспериментах многие величины определяются не непосредственно, а косвенным путём – измерением значений других величин. Так, чтобы найти плотность тела, ученые измеряют его массу, взвешивая на весах, после чего определяют объём тела, погружая его в жидкость. Плотность 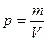выражается через массу и объём тела. Масса и объём, входящие в эту формулу, измеряются с некоторой погрешностью; это означает, что и плотность будет вычислена по формуле с некоторой погрешностью.

Выведем несколько правил, позволяющих рассчитывать погрешности величин:

1. Абсолютная погрешность суммы двух независимых величин равна сумме абсолютных погрешностей отдельных слагаемых: Δ(x + y) = Δx + Δy.

2. Абсолютная погрешность разности двух независимых величин равна сумме абсолютных погрешностей уменьшаемого и вычитаемого: Δ(x – y) = Δ x + Δ y.

3. Относительные погрешности при сложении и вычитании складывать нельзя.

4. Относительная погрешность произведения приближённо равна сумме относительных погрешностей отдельных сомножителей: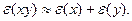

В частности,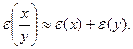

Пример 2.

Определить, какое равенство точнее: .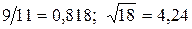

Найдем значения данных выражений с большим числом десятичных знаков. Для этого выполним следующие действия:

>> format long %длинное представление числа (15 знаков)

>> a1=9/11

a1 =

0.81818181818182

>> a2=sqrt(18)

a2 =

4.24264068711928

Затем вычислим предельные абсолютные погрешности:

>> abs(a1-0.818)

ans =

1.818181818182829e-004

>> abs(a2-4.24)

ans =

0.00264068711928

Округлим их с избытком:

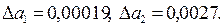
Вычислим предельные относительные погрешности:

>> 0.00019/0.818

ans =

2.322738386308069e-004

>> 0.0027/4.24

ans =

6.367924528301887e-004

Таким образом,

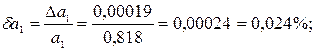
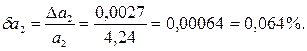
Так как 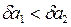, то равенство 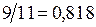является более точным.

 

Пример 3.

Округлить сомнительные цифры числа, оставив верные знаки: .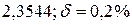

Для определения верных знаков необходимыми значениями будут являться:

· Число а;

· .

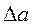Также, для определения используем неравенство 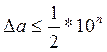, где n-разряд определяемой цифры числа а.

Пусть 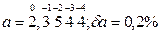; тогда .

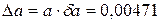(2) 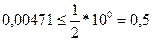- верно;

(3) 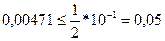- верно;

(5) 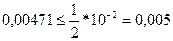- верно;

(4) 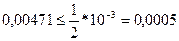- не верно => цифра является сомнительной.

В данном числе верными являются три цифры, поэтому округляем его, сохраняя эти цифры:

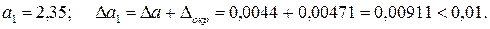
Значит, и в округленном числе 2,35 все три цифры верны.

 

Пример. Найти предельную абсолютную и относительную погрешности числа 12,384, если оно имеет только верные цифры.

Так как все пять цифр числа а =12,384 верны, то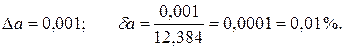

 

Пример 4.

Вычислить и определить погрешности результата 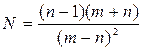, где n =3,0567(±0,0001), m =5,72(±0,02).

Имеем:

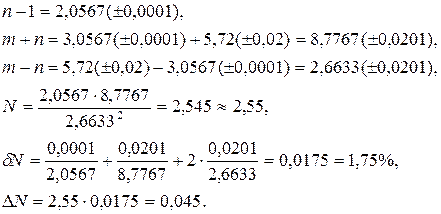
Ответ: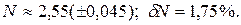

Выполнение работы

Задание 1. В ходе выполнения задания необходимо: