Примеры решения задач

1 2 3 4

ЛИНЕЙНАЯ АЛГЕБРА

МАТРИЦЫ

1.1.1. Матрицы. Операции над матрицами

Определение матрицы

Матрицей А размера

называется таблица из т·п чисел

Часто для краткости пишут А = || a_ij ||. Числа, из которых состоит матрица, называются элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент а ₂₃ находится на пересечении второй строки и третьего столбца:

Элементы а ₁₁, а ₂₂, а ₃₃, …называются главной диагональю матрицы

Если матрица А имеет размер то такую матрицу называют квадратной матрицей порядка п.

Две матрицы одинакового размера А = || a_ij || и B = || b_ij || называют равными (при этом пишут А = В), если

Упражнение 1.

Найти а ₁₂ и а ₂₃.

Решение.

Элемент а ₁₂ располагается в первой строке и втором столбце, то есть это второй элемент первой строки: а ₁₂ = -1.

Соответственно а ₂₃ – элемент, стоящий во второй строке и в третьем столбце;

а ₂₃ = -3.

Упражнение 2.

Даны матрицы

При каких a и b А=В?

Решение.

У равных матриц должны быть равными соответствующие элементы. Для элементов, заданных численно, это условие выполняется: a ₁₂ = b ₁₂ = 1,

a ₂₂ = b ₂₂ = 3. Поскольку b ₁₁ = 4, a a ₂₁ = -2, для равенства матриц А и В должны выполняться условия:

Следовательно, a = ± 2, b = -2.

Ответ: a = ± 2, b = -2.

Сумма матриц

Суммой двух матриц одинакового размера

А = || a_ij || и B = || b_ij || называют матрицу С = || с_ij || размера

такую, что

Пример 1.

Упражнение 3.

Даны матрицы

, .

Найти А+В.

Нулевой матрицей называется матрица, все элементы которой равны нулю.

Легко проверить, что выполнены следующие свойства для операции сложения матриц:

1. А+В=В+А (коммутативность), 2. (А+В)+С=А+(В+С) (ассоциативность), 3. А +0= А.

Произведением матрицы размера т 5 п А = || a_ij || на число l называют матрицу того же размера С = || с_ij || такую, что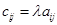

Упражнение 4.

Дана матрица

Найти матрицу С = -3 А.

Решение.

Из определения произведения матрицы на число следует, что размер матри-цы С совпадает с размером матрицы А (), а каждый элемент матрицы С равен соответствующему элементу матрицы А, умноженному на -3:

Таким образом,

Ответ: .

Нетрудно убедиться, что имеют место следующие свойства:

1. l (А+В)= l А+ l В, 2. (l + m)А= l А+ m А, 3. (lm)А= l (m А).

Разностью матриц одинакового размера А и В называется матрица А-В=А +(-1) В.

Знак суммы

Нам часто придется иметь дело с различными суммами. Удобно иметь обозначение для сумм, позволяющее записывать их более коротким способом. Этому служит знак суммирования

Из хорошо известных свойств чисел вытекают следующие свойства знака суммирования:

Произведение матриц

Умножение матрицы А = || a_ij || размера на матрицу В = || b_ij || размера определено лишь для случая, когда число столбцов матрицы А совпадает с числом строк матрицы В, т.е. когда n=l. В этом случае произведение матриц определяется следующим образом:

Произведением матриц АВ называется матрица С = || с_ij || размера

, у которой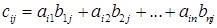

Иначе говоря, элемент c_ij равен сумме произведений элементов i -ой строки матрицы А на соответствующий элемент j -ого столбца матрицы В. С помощью знака суммирования можно записать это так:

Пример 2.

Найти произведение матриц

и .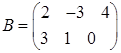

Имеем

Отметим, что произведение матриц некоммутативно, т.е. в общем случае АВ не равно ВА. В приведённом выше примере матрицу В просто нельзя даже умножить на матрицу А. Но, даже если А и В – квадратные матрицы одного порядка (тогда существуют произведения АВ и ВА), то, как показывает следующий пример, произведения АВ и ВА могут не совпадать.

Пример 3.

Пусть , .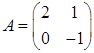

Тогда ,

Единичной матрицей называется квадратная матрица вида

Упражнение 5.

Доказать, что для любой квадратной матрицы А

АЕ=ЕА=А,

где Е – единичная матрица того же порядка, что и А.

Доказательство.

Пусть А и Е – квадратные матрицы п -го порядка, В = АЕ.

Тогда b_ij = a_i ₁ e ₁ _j + a_i ₂ e ₂ _j +... + a_ije_jj +... + a_ine_nj.

Но e_ij = 0 при i, не равном j, a e_jj = 1. Следовательно, b_ij = a_ij ·1 = a_ij. Таким образом, все элементы матрицы В равны соответствующим элементам матрицы А, то есть В = А.

Если матрица С = ЕА, то с_ij = е_i ₁ а ₁ _j + е_i ₂ а ₂ _j +... + е_iiа_ij +... + е_inа_nj = 1· a_ij = a_ij

(учитываем, что e_ii = 1, e_ij = 0 при i, не равном j). Значит, С = А. Утверждение доказано.

Приведём ряд свойств произведений матриц.

1. (АВ)С=А(ВС)

Доказательство.

Пусть размер матрицы A = || a_ij || матрицы B = || b_ij || - а матрицы

C = || c_ij || Имеем AB = || a_ij ||, где

Тогда (AB) C = || g_ij ||, где

где - элемент матрицы ВС. Тем самым, если обозначить элемент матрицы А(ВС) через g’_ij, будем иметь

2. А(В+С)=АВ+АС, (В+С)А=ВА+СА

Доказательство.

Пусть матрица A = || a_ij || имеет размер а матрицы B = ||b_ij || и C = ||c_ij|| имеют размер Тогда для элементов матрицы А (В+С)= || g_ij || имеем

Из определения произведения матриц вытекает, что АВ = || a_ij||, а АС = || b_ij||, т.е. А (В+С)= АВ+АС. Аналогично доказываем, что (В+С) А=ВА+СА.

Упражнение 1.6.

Пусть А и В – квадратные матрицы одного порядка. Вывести формулу для (А+В)² (при натуральном п под Сⁿ понимается произведение С·С·…·С).

Решение.

Используем свойства сложения и умножения матриц:

(А + В)² = (А + В)(А + В) = (А + В) А + (А + В) В = А·А + В·А + А·В +В·В =

= А ² + В·А + А·В +В ².

Заметьте, что результат может совпасть с формулой сокращенного умножения (А + В)² = А ² + 2 АВ + В ² только в том случае, если АВ = ВА. В общем случае это неверно!

Ответ: (А + В)² = А ² + В·А + А·В +В ².

Упражнение7.

Пусть А и В – квадратные матрицы одного порядка. Разложить на множители выражение АВ +2 В.

Решение.

Используем свойство единичной матрицы (см. упражнение 5):

АЕ = ЕА = А.

Следовательно, В = ЕВ. Тогда АВ + 2 В = АВ + (2 Е) В = (А + 2 Е) В

(использовано свойство 2 произведения матриц).

Ответ: АВ + 2 В = (А + 2 Е) В.

Упражнение 8.

Пусть А, В и С – квадратные матрицы одного порядка. Разложить на множители выражение А ² С +АС ².

Решение.

Поскольку А ² = А·А, С ² = С·С, запишем заданный матричный многочлен в виде: А ² С +АС ² = А·А·С +А·С·С и воспользуемся свойствами произведения матриц:

А·А·С +А·С·С = А (А·С +С·С) = А ((А + С) С) = А (А + С) С.

Ответ: А ² С +АС ² = А (А + С) С.

Упражнение 9.

Найти АВ и ВА.

Решение.

Определим размеры матрицы А: и В: Следовательно, существуют оба произведения: и АВ, и ВА, причем размер матрицы С = АВ: а матрицы D = BA:

Вычислим элементы матрицы С:

Таким образом, матрица С имеет вид:

Матрица D состоит из единственного элемента:

Тогда .

Ответ: , .

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПО ТЕМЕ «Операции над матрицами»

Задача 1.

Найти матрицу 5А – 2В, если

Указание

Используя операции умножения матрицы на число и сложения матриц, найдите сначала матрицы 5 А и -2 В, а затем их сумму.

Решение

Используем определения линейных операций надматрицами:

Ответ: 5А – 2В .

Задача 2.

Найти х, у и т, если

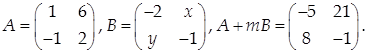
Указание

Используя операции умножения матрицы на число и сложения матриц, найдите элементы матрицы А + тВ, а затем приравняйте их соответствующим элементам матрицы

Решение

Если

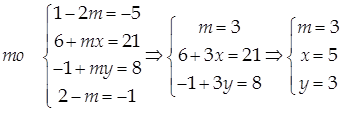Ответ: х = 5, у = 3, т = 3.

Задача 3.

Найти АВ и ВА, если

Указание

Проверьте возможность перемножения матриц, определив их размерность, а затем используйте определение произведения матриц.

Решение

Проверим возможность перемножения матриц, определив их размерность.

A [ 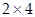], B [ ]. Следовательно, n = l = 4, m = k = 2, поэтому матрицы АВ и ВА существуют, причем АВ [ ], BA [ ].

Для вычисления элементов матрицы С = АВ элементы строк матрицы А умножаются на соответствующие элементы столбцов матрицы В:

с ₁₁ = 2 · 2 + (-2)(-1) + 1 · 1 + 0 · 2 = 9

(сумма произведений элементов первой строки А на элементы первого столбца В; первый индекс вычисляемого элемента задает номер строки А, второй индекс – номер столбца В);

с ₁₂ = 2 · 2 + (-2) · 0 + 1 · 1 + 0 · 4 = 5;

с ₂₁ = -3 · 3 + 1 · (-1) + (-1) · 1 + 1 · 2 = -9;

с ₂₂ = -3 · 2 + 1 · 0 + (-1_ · 1 + 1 · 4 = -3.

Следовательно,

При вычислении элементов матрицы D = BA элементы строк В умножаются на элементы столбцов А:

d ₁₁ = 3 · 2 + 2 · (-3) = 0; d ₁₂ = 3 · (-2) + 2 · 1 = -4; d ₁₃ = 3 · 1 + 2 · (-1) = 1;

d ₁₄ = 3 · 0 + 2 · 1 = 2; d ₂₁ = -1 · 2 + 0 · (-3) = -2; d ₂₂ = -1 · (-2) + 0 · 1 = 2;

d ₂₃ = -1 · 1 + 0 · (-1) = -1; d ₂₄ = -1 · 0 + 0 · 1 = 0; d ₃₁ = 1 · 2 + 1 · (-3) = -1;

d ₃₂ = 1 · (-2) + 1 · 1 = -1; d ₃₃ = 1 · 1 + 1 · (-1) = 0; d ₃₄ = 1 · 0 + 1 · 1 = 1;

d ₄₁ = 2 · 2 + 4 · (-3) = -8; d ₄₂ = 2 · (-2) + 4 · 1 = 0; d ₄₃ = 2 · 1 + 4 · (-1) = -2;

d ₄₄ = 2 · 0 + 4 · 1 = 4.

Таким образом,

Ответ:

Задача 4.

Выяснить, можно ли умножить друг на друга матрицы

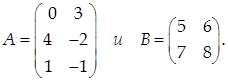
Если произведение существует, вычислить его.

Указание

Проверьте возможность перемножения матриц, определив их размерность, а затем (в случае, если произведение АВ или ВА существует) найдите его, используя определение произведения матриц.

Решение

Сравним размерности матриц А и В: A [ ], B [ ]. Следовательно, поэтому произведение АВ [ ] существует, а произведение ВА – нет.

Найдем элементы АВ:

(ab)₁₁ = 0 · 5 + 3 · 7 = 21; (ab)₁₂ = 0 · 6 + 3 · 8 = 24; (ab)₂₁ = 4 · 5 – 2 · 7 = 6;

(ab)₂₂ = 4 · 6 – 2 · 8 = 8; (ab)₃₁ = 1 · 5 – 1 · 7 = -2; (ab)₃₂ = 1 · 6 – 1 · 8 = -2.

Ответ: ВА не существует.

Задача 5.

Вычислить матричный многочлен А² – 3 А, где

Указание

Найдите произведение АА и матрицу -3 А, а затем сложите полученные матрицы.

Решение

Поскольку А ² = А · А, умножим матрицу А на себя по правилу умножения матриц. А – квадратная матрица 2-го порядка, поэтому А ² – тоже квадратная матрица той же размерности.

Найдем элементы матрицы С = А ²:

с ₁₁ = -2·(-2) + 1 · 0 = -4;

с ₁₂ = -2·1 + 1 · 3 = 1;

с ₂₁ = 0·(-2) + 3 · 0 = 0;

с ₂₂ = 0·1 + 3 · 3 = 9.

Итак,

Теперь вычислим элементы матрицы D = -3 A. Для этого все элементы матрицы А умножим на -3:

Следовательно,

Ответ:

Задача 6.

Найти матрицу Х из уравнения Х ² = А, где

Указание

Из определения операции умножения матриц следует, что Х – квадратная матрица 2-го порядка.

Пусть

тогда, приравнивая элементы произведения Х· Х соответствующим элементам А, получим систему уравнений для определения элементов матрицы Х.

Решение

Из определения операции умножения матриц следует, что Х – квадратная матрица 2-го порядка.

Пусть

тогда, приравнивая элементы произведения Х· Х соответствующим элементам А, получим систему уравнений

Разделив левую и правую части второго уравнения на соответствующие части третьего, получим, что откуда b = -c. Подставим это выражение для b в систему: