1. Для любой квадратной матрицы порядка п  |
Тем самым определитель может быть вычислен не только с помощью разложения по первой строке (как в исходном определении), но и с помощью разложения по первому столбцу.
Доказательство
Для матриц второго порядка это свойство легко проверяется. Допустим, что доказываемое свойство имеет место для матриц порядка п – 1. Докажем, что оно выполняется для матриц порядка п. В силу определения имеем:
 (1)
(1)
Пользуясь предположением индукции, вычислим M 1 j, 2 ≤ j ≤ n, с помощью разложения по первому столбцу. Тогда

где (M 1 j) i 1 – определитель, получаемый из матрицы А вычеркиванием 1-ой строки и j -го столбца, а также i -й строки и 1-го столбца. Подставляя это выражение в (1), получаем:
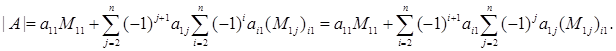
В силу того, что

имеем:

Треугольной матрицей называется матрица вида
 (2)
(2)
Упражнение 5.
Вычислим определитель треугольной матрицы, разлагая его по первому столбцу. В силу того, что в первом столбце только один элемент отличен от нуля, имеем:

Продолжая этот процесс, получим:

Таким образом, определитель треугольной матрицы равен произведению элементов, стоящих на главной диагонали.
Матрицей, транспонированной к матрице А = || aij || размера т×п, называется матрица АТ = || bij || размера п×т, где bij = aji. Иными словами, чтобы из исходной матрицы получить транспонированную, надо ее строки поставить в соответствующие столбцы.
Пример 5. Пусть

Тогда
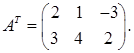
Упражнение 6. Для

найти АТ и (А 2) Т.
Решение.

Матрицу АТ получим из матрицы А следующим образом: элементы 1-ой строки матрицы А образуют 1-ый столбец матрицы АТ, элементы 2-ой строки А – 2-ой столбец АТ, элементы 3-ей строки А – 3-ий столбец АТ:

Найдем матрицу А 2:

Тогда 
| 2. Для любой квадратной матрицы А | A | = | AT |. |
Доказательство.
Для матриц второго порядка это свойство легко проверяется. Допустим, что доказываемое свойство имеет место для матриц порядка п – 1. Докажем, что оно выполняется для матриц порядка п. Разложим определитель матрицы АТ по первому столбцу:

где M 1 i * - определитель, получаемый из матрицы АТ вычеркиванием i -ой строки и 1-го столбца. В силу предположения индукции M 1 i *= M 1 i. Тем самым

Из свойства 2 вытекает равноправность строк и столбцов, т.е. если какое-либо утверждение об определителе доказано относительно строк, то оно верно и относительно столбцов. Далее в силу сказанного все свойства будут доказываться лишь для строк.
| 3. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель изменит знак, а модуль его значения не изменится. |
Доказательство.
Докажем сначала это свойство для двух соседних строк. Снова воспользуемся методом полной индукции. Для матрицы 2-го порядка это свойство легко проверяется. Предположим, что перестановка двух соседних строк меняет знак определителя порядка п – 1. Пусть в матрице

переставляются строки с номерами k и k + 1. Матрицу с переставленными строками обозначим через

Напишем разложение определителей этих двух матриц по первому столбцу:

При i ≠ k,k + 1 в силу предположения индукции Ni 1 = - Mi 1. Остается заметить, что Nk 1 = Mk +1,1, a Nk +1,1 = Mk 1. Тогда

Пусть теперь в матрице переставляются строки с номерами i и j, i < j. Перестановку этих строк можно осуществить, переставляя только соседние строки, следующим образом. Сначала j -я строка последовательно переставляется с j – i строками, стоящими над ней, а затем i -я строка последовательно переставляется с j – i - 1 строками, стоящими под ней. Всего будет переставлено 2(j – i) – 1 соседних строк. Поэтому определитель нечетное число раз будет менять знак и в результате поменяет знак.
Следствие 2.1. Если у квадратной матрицы А имеются две одинаковые строки (столбца), то | A | = 0.
Доказательство.
Пусть у матрицы А имеются две одинаковые строки. Поменяв их местами, получим ту же самую матрицу, но по свойству 3 ее определитель должен поменять знак, т.е. получаем, что | A | = - | A |, что возможно только при | A | = 0.
4. Определитель матрицы может быть разложен по любой строке или столбцу, то есть имеют место равенства  |
Доказательство.
Как уже отмечалось, в силу равноправности строк и столбцов достаточно доказать разложимость по любой строке. Положим

Матрицу В можно получить из матрицы А, последовательно меняя k -ю строку со строками, находящимися над ней. Поскольку таких перестановок будет k – 1 (столько строк лежит выше k -ой строки), то по свойству 3
| A | = (-1) k – 1 | B |.
Вычислим теперь определитель матрицы В с помощью разложения по первой строке:

Нетрудно убедиться, что N 1 j = Mkj, j = 1,..., n. Поэтому

Алгебраическим дополнением элемента aij называется величина
| Aij = (-1) i+jMij. |
 Равенства в свойстве 4 могут быть записаны через алгебраические дополнения:
Равенства в свойстве 4 могут быть записаны через алгебраические дополнения:
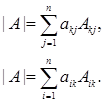 (5)
(5)
Пример 6. Вычислим определитель из примера 4, разлагая его по третьему столбцу (в нем больше всего нулей):

Упражнение 7. Вычислить определитель

Решение.
Наиболее удобно вычислять этот определитель разложением по 3-му столбцу (при этом потребуется вычислить только один определитель 3-го порядка):

Линейной комбинацией матриц А 1, …, Ат одинакового размера называется матрица А = l 1 А 1 + … + lтАт, где l 1, …, lт – некоторые числа. В случае, если матрицы А 1, …, Ат имеют размеры 1 × п, говорят о линейной комбинации строк, а если размеры этих матриц п × 1, то говорят о линейной комбинации столбцов.
| 5. Если у квадратной матрицы А i-я строка (столбец) есть линейная комбинация строк (столбцов) Аi′ и Аi′′, т.е. имеет вид l 1 Аi′ + l 2 Ai′′, то | A | = l 1| A ′| + l 2| A ′′|, где А′ и А′′ - матрицы, у которых i-е строки (столбцы) заменены на Аi′ и Аi′′ соответственно. |
Доказательство.
Пусть

Тогда, разлагая определитель матрицы А по i -ой строке, будем иметь:

Положив в этом свойстве l 2 = 0, получаем
Следствие 2.2. При умножении строки (столбца) квадратной матрицы на число ее определитель умножается на это число.
Упражнение 8. Пусть А – квадратная матрица порядка п с определителем | A |, a l – число. Найти | lA |.
Решение.
Если 
Поэтому, используя следствие 2.2, можно сказать, что определитель | lA | получается из определителя | A | при умножении каждой из п строк матрицы на число l, следовательно, | lA | = ln | A |.
Умножив строку (столбец) на l = 0, из следствия 2.2 получаем
Следствие 2.3. Если в квадратной матрице А имеется строка (столбец) с нулевыми элементами, то |A| = 0.
| 6. Определитель не изменится, если к любой строке (столбцу) прибавить другую строку (столбец), умноженную на произвольное число. |
Доказательство.
Предположим, что к i -ой строке матрицы A = || aij || прибавлена k -ая строка, умноженная на число l. Тогда по свойству 5, следствию 2.2 и следствию 2.1

Пример 7. Вычислим определитель матрицы

с помощью свойства 6. Вычтем из третьего столбца первый, а к четвертому столбцу прибавим первый, умноженный на 2. После этого разложим полученный определитель по второй строке. Имеем:

В определителе третьего порядка вынесем множитель 2 из второго столбца: 
Теперь прибавим ко второй строке первую, умноженную на 2, и вычтем из третьей строки первую:

Упражнение 9. Вычислить определитель матрицы

пользуясь свойствами определителей.
Решение.
Приведем определитель матрицы А к треугольному виду. Для этого поменяем в нем местами 1-ую и 2-ую строки (при этом по свойству 3 определитель поменяет знак), а затем 1-ый и 2-ой столбец (определитель вновь поменяет знак, то есть окажется равным | A |). Получим:

Теперь вычтем из 2-ой строки 1-ую, умноженную на 2 (по свойству 6 определитель при этом не изменится):

Преобразуем определитель так, чтобы элемент а 42 стал равным нулю. Для этого умножим 4-ю строку на 5 (тем самым по следствию 2.2 весь определитель умножится на 5) и вычтем из нее 2-ую строку, умноженную на 2:
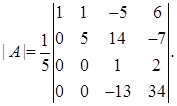
И наконец, прибавим к 4-ой строке 3-ю, умноженную на 13 (напомним еще раз свойство 6: такое преобразование не меняет значения определителя):

(при вычислении определителя треугольной матрицы использован результат, полученный в упражнении 2.5). Итак, | A | = 60.
 2017-11-01
2017-11-01 1360
1360
