Определители 2-го и 3-го порядков

Каждой квадратной матрице можно сопоставить некоторое число, называемое определителем матрицы и обозначаемое через | A |. Прежде чем дать общее определение этого понятия, определим его для матриц 2-го и 3-го порядков.

Определителем матрицы 2-го порядка называется число .

Пример 1.

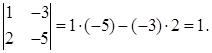
Упражнение 1. Найти определители

Решение.

Определителем матрицы 3-го порядка называется число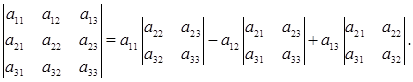

Пример 2.

При раскрытии определителей 2-го порядка выражение для определителя 3-го порядка может быть записано в общем случае в виде

Для вычисления определителя по этой формуле существует следующая геометрическая схема, называемая «правилом треугольников». Первые три слагаемых находятся перемножением элементов, стоящих на главной диагонали, и элементов, стоящих в вершинах треугольников с основаниями, параллельными главной диагонали:

Остальные три слагаемых (с минусами) получаются по аналогичной схеме:

Упражнение 2. Найти определители

Решение.

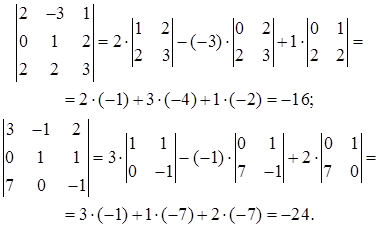
Определитель п -го порядка

Пусть дана квадратная матрица А. Минором М_ij называется определитель матрицы, получаемой из матрицы А вычеркиванием i -ой строки и j -го столбца.

Пример 3. Если

то

Упражнение 3. Найти М ₃₂ и М ₃₁ для матрицы

Решение.

Минор М ₃₂ получаем, вычеркнув из матрицы А 3-ю строку и 2-ой столбец:

Для вычисления минора М ₃₁ вычеркиваем из матрицы А 3-ю строку и 1-ый столбец:

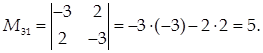
Общее понятие определителя дадим с помощью рекуррентной схемы, а именно, считая, что понятие определителя известно для матриц п –1-го порядка, дадим его для матриц п -го порядка (фактически так и вводилось понятие определителя для матриц 3-го порядка).

Определителем матрицы А = || aij || порядка п называется число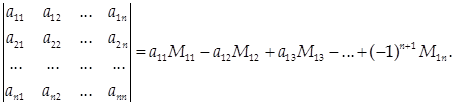

Используя знак суммы, это определение можно записать в виде:

Пример 4.

Упражнение 4. Вычислить

Решение.