Лабораторная работа № 1. Модели множественной регрессии

Ю.В. Зайцева

 

Лабораторные для магистров

(ЭКОНОМЕТРИКА)

(Математические методы прогнозирования)

Волгоград 2017

Лабораторная работа № 1. Модели множественной регрессии

Задание 1. (Построение модели линейной множественной регрессии в пакете Excel). Имеются данные о потреблении мяса в США B в 1980 – 2007 годах (фунты на душу населения), и его зависимости от цены P (центы за фунт) и личного располагаемого дохода YD (тысячи долларов в расчете на душу населения).

1. Скопировать из файла данные для своего варианта. Должно получиться 3 столбца YD, B, P.

2. Постройте линейную модель множественной регрессии, объясняющую динамику потребления мяса в США в зависимости от цены и личного располагаемого дохода.

Для этого в excel 2003 выберите в меню Данные – Анализ данных – Регрессия. Если этой команды нет в меню, необходимо загрузить надстройку Пакет анализа через команду Сервис.

В excel 2007

1) нажмите кнопку Microsoft Office , а затем щелкните Параметры Excel.

2) Выберите команду Надстройки и в окне Управление выберите пункт Надстройки Excel.

3) Нажмите кнопку Перейти.

4) В окне Доступные надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.

Если Пакет анализа отсутствует в списке поля Доступные надстройки, то для проведения поиска нажмите кнопку Обзор.

В случае появления сообщения о том, что пакет статистического анализа не установлен на компьютере и предложения установить его, нажмите кнопку Да.

5) После загрузки пакета анализа в группе Анализ на вкладке Данные становится доступной команда Анализ данных.

В поле Входной интервал Y выделите столбец В вместе с заголовком. В поле Входной интервал Х выделите столбцы YD и P (также вместе с заголовком). Поставьте галочку в поле Метки. Тогда Excel поймет, что в первой строке находятся названия переменных. Должно получится примерно следующее:

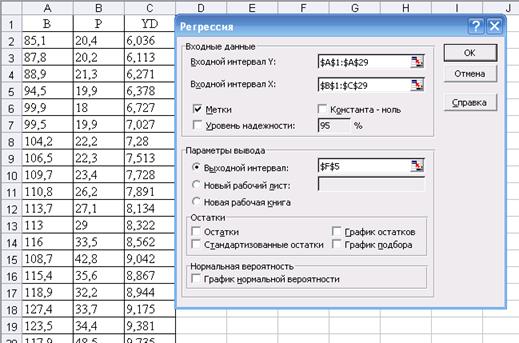
Найдите столбец с коэффициентами и по этому столбцу выпишите уравнение регрессии. Например, по таблице

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	37,5	10,0	3,7	0,0	16,9	58,2
P	-0,9	0,2	-5,4	0,0	-1,2	-0,5
YD	11,9	1,8	6,7	0,0	8,3	15,5

 

Выписываем уравнение B=37.5-0.9P+11.9YD

3. Дайте подробную интерпретацию коэффициентам полученной модели.

В нашем примере:

с ростом цены на 1 цент за фунт потребление мяса сокращается на 0,9 фунтов на душу населения (при неизменном доходе)

с ростом дохода на 1 тысячу долларов в расчете на душу населения потребление мяса увеличивается на 11,9 фунтов на душу населения (при неизменной цене)

4. Чему равен коэффициент детерминации модели? Что он показывает?

В нашем примере смотрим на таблицу

Регрессионная статистика
Множественный R	0,81
R-квадрат	0,66
Нормированный R-квадрат	0,63
Стандартная ошибка	6,08
Наблюдения

Коэффициент детерминации равен 0,66. Это означает, что 66% вариации потребления мяса объясняется вариацией в доходах и в цене и 34% иными факторами, не включенными в модель.

5. Проверьте значимость всей модели в целом.

В нашем примере обращаем внимание на таблицу

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		1778,6736	889,33681	24,05287	1,496E-06
Остаток		924,35639	36,974255
Итого		2703,03

Значимость F - это вероятность того, что полученная зависимость случайна. При значимости больше 0,05 обычно считают, что построенная зависимость незначима. Моделью нельзя пользоваться для прогнозирования.

Так как 1,496E-06<0,05, модель значима, т.е. построенная зависимость не случайна, потребление мяса существенно зависит от цены и дохода.

6. Проверьте значимость отдельных коэффициентов модели.

В нашем примере обращаем внимание на таблицу

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	37,5	10,0	3,7	0,0	16,9	58,2
P	-0,9	0,2	-5,4	0,0	-1,2	-0,5
YD	11,9	1,8	6,7	0,0	8,3	15,5

Р-значение - это вероятность того, что соответствующая переменная не влияет на зависимую переменную y. При Р-значении больше 0,05 обычно считают, что соответствующая переменная незначима и ее можно исключить из уравнения регрессии.

Так как для обеих переменных Р и YD Р-значение=0,0<0.05, обе эти переменные значимы. Это означает, что обе переменные влияют на потребление мяса.

 

7. Постройте модели парной линейной регрессии, в которых потребление мяса в США объясняется изменением только одного фактора. Сравните их с моделью множественной регрессии: в чем заключается преимущество модели множественной регрессии?

Для ответа на вопрос обратите внимание на интерпретацию коэффициентов и на коэффициент детерминации.

8. Рассчитайте средние эластичности объема потребления мяса по цене и по доходу. Для расчета применяется формула 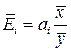. Дайте интерпретацию полученным эластичностям (вспомните микроэкономику и математику 1 курса). Сравните силу влияния каждого из факторов на потребление мяса.

9. Постройте прогноз потребления мяса для цены 30 центов за фунт и личного располагаемого дохода 7 тыс. долл.

Задание 2. (Построение модели степенной множественной регрессии в пакете Excel).

1. Создайте столбцы, содержащие логарифмы исходных данных.

2. Постройте степенную модель множественной регрессии, объясняющую динамику потребления мяса в США вида

.

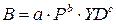Если прологарифмировать эту модель, мы получим 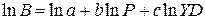(если непонятно как такое получилось, вспоминаем школьную математику – свойства логарифмов). Модель в логарифмах является линейной, а значит ее можно построить в Excel, задав в качестве зависимой переменной ln(B), а в качестве независимых ln(P) и ln(YD).

 

Запишите полученное уравнение. Не забудьте от модели в логарифмах перейти к исходной модели.

В нашем примере получим таблицу

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	3,59	0,14	25,44	0,00	3,30	3,88
ln(P)	-0,34	0,06	-5,54	0,00	-0,47	-0,22
ln(YD)	1,07	0,15	7,22	0,00	0,77	1,38

 

Уравнение в логарифмах:

Ln(B)=3.59-0.34ln(P)+1.07ln(YD)

Исходная модель:

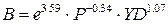
или

3. Дайте интерпретацию коэффициентам степенной модели.

Вспоминаем чем являются показатели степени в степенной модели

4. Проверьте значимость отдельных коэффициентов модели и всей модели в целом.

Здесь все также, как и в линейной модели

5. Рассчитайте эластичности объема потребления мяса по цене и по доходу. Дайте интерпретацию полученным эластичностям. Сравните силу влияния каждого из факторов на потребление мяса.

Если сделали пункт 3, то здесь все просто.

6. Постройте прогноз потребления мяса для цены 30 центов за фунт и личного располагаемого дохода 7 тыс. долл. по степенной модели.

7. Какую из двух моделей вы бы выбрали?