2017-11-01
388
Алгоритм оценивания коэффициентов синтезирован с помощью теории рекуррентной линейной фильтрации.
Предположим, что каждая компонента вектора 
является медленно меняющимся случайным процессом. Тогда ее можно аппроксимировать авторегрессией первого порядка 
, где 
- матрица размером 
, 
, 
- единичная матрица размером 
,«*»- знак комплексно сопряженной величины.
Таким образом, получим модель:
(3)
Пусть 
.
Требуется по входной последовательности 
и тестовому сигналу 
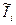синтезировать алгоритм оценивания вектора коэффициентов эквалайзера по критерию (2) минимума средней квадратической ошибки (СКО). Полученные оценки должны быть асимптотически несмещенными: 
, асимптотически эффективными: 
и состоятельными: 
. Здесь 
- оператор математического ожидания, 
- вероятность.
Используя модель (3) поставленную задачу можно решить модифицированным методом наименьших квадратов (МНК), который основывается на минимизации функционала Тихонова А.Н.:
(4)
Здесь 
- евклидова норма, 
, 
- скалярное произведение.
Минимизируя (4), получим выражение для оценок комплексного вектора коэффициентов эквалайзера:
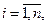(5)
,
.
- ковариационная матрица ошибок экстраполяции, 
- ковариационная матрица ошибок фильтрации.
Начальные условия: 
- из априорных сведений, - единичная матрица размером .
 | |||||
 | | ||||
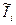
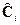
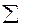
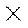
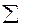
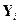
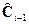
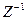
Рис. 4. Структурная схема алгоритма (5).
Достоинство алгоритма: быстрая сходимость.
Недостатки: 1)сложность; 2) чувствительность к шуму, который накапливается при рекуррентных операциях и может вызвать нестабильность алгоритма.
