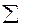Применение эквалайзера в модемах позволяет значительно повысить эффективность использования полосы при передаче данных по телефонным и радиоканалам.
Существует несколько алгоритмов синтеза адаптивных эквалайзеров [1]. В лабораторной работе рассматриваются рекуррентные алгоритмы минимальных квадратов для адаптивного выравнивания - алгоритм Калмана и алгоритм кратчайшего спуска (градиентный метод). В основе обоих алгоритмов лежит метод наименьших квадратов. Рекуррентные процедуры более просты и требуют меньший объем памяти при реализации на цифровой схемотехнической базе.
Рассматриваемый эквалайзер построен на базе трансверсального фильтра (линейный эквалайзер) с числом линий задержек N (см. рис 3).
 |




|

|

|



|
 1
1 




|
|
|
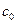

 2
2  |  |  | |||||||||
 | |||||||||||
 | |||||||||||
 | |||||||||||









|


 выход
выход
 |


Рис. 3. Структурная схема эквалайзера.
На вход эквалайзера поступают отсчеты  ,
,  (
( ) дискретизированного по времени комплексного сигнала
) дискретизированного по времени комплексного сигнала 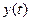 (см. формулу (1)).
(см. формулу (1)).
 ,
,  - оператор математического ожидания. Сначала ключ находится в положении «1». На этом этапе происходит обучение по известной информационной последовательности, т.е. оцениваются коэффициенты трансверсального фильтра так, чтобы разность
- оператор математического ожидания. Сначала ключ находится в положении «1». На этом этапе происходит обучение по известной информационной последовательности, т.е. оцениваются коэффициенты трансверсального фильтра так, чтобы разность 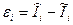 между сигналом на выходе фильтра
между сигналом на выходе фильтра  , где
, где  ,
,  -вектор комплексных коэффициентов, «Т» - знак транспонирования, и тестовой последовательностью свести к минимуму.
-вектор комплексных коэффициентов, «Т» - знак транспонирования, и тестовой последовательностью свести к минимуму.
 (2)
(2)
После периода обучения, когда коэффициенты эквалайзера сошлись к своим оптимальным значениям, ключ переходит в положении «2». На этом этапе сигнал 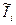 - продетектированные решения, которые являются выходом эквалайзера. Они достаточно надежны, поэтому их можно дальше использовать для адаптации коэффициентов.
- продетектированные решения, которые являются выходом эквалайзера. Они достаточно надежны, поэтому их можно дальше использовать для адаптации коэффициентов.
 2017-11-01
2017-11-01 1016
1016