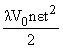Задача 1. В какое ядро превратится ядро 212Bi, испустив α-частицу. Записать уравнение ядерной реакции.
Теория. Атомные ядра (нуклиды) состоят из элементарных частиц двух видов — протонов и нейтронов. Эти частицы объединяют общим названием нуклоны. Число протонов в ядре называется атомным номером и обозначается буквой Z. Общею число нуклонов в ядре называется массовым числом и обозначается буквой А. Для характеристики данного нуклида используют символ его химического элемента X и указывают А и Z: AZX, 
Радиоактивность — процесс самопроизвольного превращения одних атомных ядер в другие, сопровождающийся испусканием одной или нескольких частиц. Атомы, подверженные таким превращениям, называют радиоактивными или радионуклидами. Основные виды радиоактивного распада — альфа ( ), бета (
), бета ( ) и спонтанное деление ядер.
) и спонтанное деление ядер.
Альфа—распад заключается в самопроизвольном испускании ядром а— частицы (ядра гелия 
 He). Схема
He). Схема  —распада:
—распада: 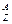



Бета — распадом называется процесс самопроизвольного превращения радиоактивного ядра в изобарное с испусканием электрона или позитрона. Известны три вида бета распада: электронный ( —распад), позитронный(
—распад), позитронный( — распад) распады и электронный захват (k—захват). Схемы
— распад) распады и электронный захват (k—захват). Схемы  —распадов:
—распадов:


k—захват: 

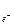

Здесь e -  , e + - символы электрона и позитрона,
, e + - символы электрона и позитрона,  — символы нейтрино и антинейтрино.
— символы нейтрино и антинейтрино.
Решение. Обозначим неизвестное ядро символом  . Так как при
. Так как при  — распаде атомный номер изменяется на -2, а массовое число на -4, то Z=83-2=81, А=212-4=208. Элемент с порядковым номером 81 в периодической системе - таллий. Следовательно, ядро 212Bi превратится в ядро 208Tl. Уравнение реакции имеет вид:
— распаде атомный номер изменяется на -2, а массовое число на -4, то Z=83-2=81, А=212-4=208. Элемент с порядковым номером 81 в периодической системе - таллий. Следовательно, ядро 212Bi превратится в ядро 208Tl. Уравнение реакции имеет вид:
 21283Bi→20881Tl +42He.
21283Bi→20881Tl +42He.
Задача 2. Какая доля начального количества атомов распадется за два года в радиоактивном изотопе 228Ra.. Период полураспада 228Ra принять равным 5 лет.
Теория. Закон радиоактивного распада N = N  или dN =
или dN =  Ndt
Ndt  , где N0 - число ядер в начальный момент времени (t =0), N - число ядер, оставшихся к моменту времени t. dN - число ядер, распавшихся за малый интервал времени dt,
, где N0 - число ядер в начальный момент времени (t =0), N - число ядер, оставшихся к моменту времени t. dN - число ядер, распавшихся за малый интервал времени dt,  ,— постоянная радиоактивного распада (вероятность распада ядра в единицу времени).
,— постоянная радиоактивного распада (вероятность распада ядра в единицу времени).
Число ядер, распавшихся за время t.  . Связь между периодом полураспада Т
. Связь между периодом полураспада Т  и постоянной распада Т
и постоянной распада Т  . Связь между постоянной распада и средним временем жизни ядра
. Связь между постоянной распада и средним временем жизни ядра 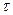
 .
.
Решение. Доля распавшихся атомов — это отношение числа распавшихся атомов  к начальному числу атомов
к начальному числу атомов  . Согласно закону радиоактивного распада
. Согласно закону радиоактивного распада  , где
, где  -постоянная распада.
-постоянная распада.  . λ=ln2/T1/2. е=2,72.
. λ=ln2/T1/2. е=2,72.
∆N/N0=1-2,72-(0,693/5)∙2=0,242.
Задача 3. Сколько слоев половинного ослабления требуется, чтобы уменьшить интенсивность узкого пучка γ—квантов в 10 раз?
Теория. Проходя через вещество, радиоактивные излучения взаимодействуют с атомами вещества. Механизм взаимодействия каждого вида ядерного излучения различен, но в конечном итоге, прохождение всех видов радиоактивных излучений через вещество приводит к ионизации атомов среды. В связи с этим радиоактивные излучения называют ионизирующими. Различают непосредственно ионизирующее и косвенно ионизирующее излучения. Непосредственно ионизирующее излучение — это излучение, состоящее из заряженных частиц, имеющих кинетическую энергию, достаточную для ионизации. Т.е.  — и
— и  — излучения относятся к непосредственно ионизирующему излучению. Косвенно ионизирующее излучение — это излучение, состоящее. из незаряженных частиц (γ -излучен не), которые в результате взаимодействия с веществом могут создавать непосредственно — ионизирующее излучение.
— излучения относятся к непосредственно ионизирующему излучению. Косвенно ионизирующее излучение — это излучение, состоящее. из незаряженных частиц (γ -излучен не), которые в результате взаимодействия с веществом могут создавать непосредственно — ионизирующее излучение.
Наибольшей проникающей способностью обладает  -излучение, наименьшей —
-излучение, наименьшей —  — излучение. В биологической ткани проникающая способность
— излучение. В биологической ткани проникающая способность  -частиц с энергией 1 МэВ имеет порядок величины 10
-частиц с энергией 1 МэВ имеет порядок величины 10  м,
м,  частиц - 10
частиц - 10  м, а
м, а  - квантов - десятки метров.
- квантов - десятки метров.
Закон ослабления узкого моноэнергетического пучка  -квантов при прохождении через вещество
-квантов при прохождении через вещество  , где
, где  - поток
- поток  -квантов в веществе на глубине
-квантов в веществе на глубине  ,
,  - поток
- поток  - квантов, падающих на вещество,
- квантов, падающих на вещество, 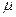 - литейный коэффициент ослабления.
- литейный коэффициент ослабления.
Слоем половинного ослабления называется слой вещества, толщина X  которого такая, что поток проходящих через него
которого такая, что поток проходящих через него  — квантов уменьшается в два раза. Связь между толщиной слоя половинного ослабления и линейным коэффициентом ослабления
— квантов уменьшается в два раза. Связь между толщиной слоя половинного ослабления и линейным коэффициентом ослабления 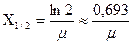
Решение. Закон ослабления узкого пучка γ-квантов слоем вещества толщиной X
n=n0∙е-µх (1) n – поток γ-квантов в веществе на глубине х, n0 – поток γ-квантов, падающих на вещество, µ - линейный коэф-т ослабления.
Слой половинного ослабления – это слой вещества, толщина х1/2 которого такая, что поток проходящих через него γ—квантов снижается в 2 раза. По условию n0/n= 10. Связь между линейным коэффициентом ослабления и толщиной Х1/2 слоя половинного ослабления х1/2 = 1n2/µ =0,693/µ. (2). Величина х/х1/2=k – искомое число половинного ослабления.
Из уравнения (1) находим х=ln(n/n0)/(-µ). (3).
Из уравнений (2) и (3) находим k= х/ х1/2=ln10/0,693=2,303/0,693=3,323.
Задача 4. Определить начальную активность А0 радиоактивного препарата 204Tl массой 0,2 кг, а так же его активность А через 150 дней. Период полураспада 204Tl принять равным 4 суток.
Теория. Активность А радиоактивного источника — число радиоактивных распадов. происходящих в источнике за единицу времени. Если в источнике за время  распадается
распадается  атомов, то
атомов, то  , где
, где  — постоянная распада,
— постоянная распада,  — число атомов радиоактивного изотопа, равное
— число атомов радиоактивного изотопа, равное  , где m — масса изотопа, M— его молярная масса, NA — число Авогадро.
, где m — масса изотопа, M— его молярная масса, NA — число Авогадро.
Единица активности в системе СИ — беккерель (Бк). Один беккерель равен одному распаду в секунду. Внесистемная единица активности — кюри (Кu). I Ku =3.7 ∙10ю Бк.
Активность источника с течением времени уменьшается по закону А  , где А
, где А  —активность в начальный момент времени (t=0), А — активность в момент времени t.
—активность в начальный момент времени (t=0), А — активность в момент времени t.
Активность радиоактивного источника, приходящаяся на единицу его массы, называется удельной массовой активностью А  . A
. A 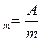 , где m - масса источника.
, где m - масса источника.
Активность источника, приходящаяся на единицу объема, называется удельной объемной активностью  ,
,  , где V — объем источника.
, где V — объем источника.
Активность источника, приходящаяся на единицу его поверхности, называется удельной поверхностной активностью А  .
.
Удельная массовая активность в системе СИ измеряется в Бк/кг, А  — в Бк/м3, А
— в Бк/м3, А  — в Бк/м2. Наряду с этими единицами часто применяют внесистемные. Например, удельную поверхностную активность А
— в Бк/м2. Наряду с этими единицами часто применяют внесистемные. Например, удельную поверхностную активность А  измеряют в Кu/км2. 1 Кu/км2 = 3,7*10
измеряют в Кu/км2. 1 Кu/км2 = 3,7*10  Бк/м2 = 37кБк/м2.
Бк/м2 = 37кБк/м2.
Решение. Начальная активность А0=λN0 (4), где λ- постоянная распада.
λ=ln2/T1/2 (5).
N0 - начальное число радиоактивных атомов. N0=NA∙(m/M) (6), где NA - число Авогадро, М - молярная масса. Подставив в (4) (5) и (6), получим A0=(m/M)∙(ln2/T1/2)∙NA. Активность спустя время t равно  (7). Учитывая, что T1/2=4 су ток=4сут∙24ч∙3600с=345600=3,5∙105с; m=0,2 кг=0,2∙103г; ln2=0,693; NA=6,02∙1023 моль-1; M=204г∙моль-1, получаем А0=(0,2∙103/204)∙(0,693/3,5∙105)∙6,02∙1023=1,2∙1018Бк.
(7). Учитывая, что T1/2=4 су ток=4сут∙24ч∙3600с=345600=3,5∙105с; m=0,2 кг=0,2∙103г; ln2=0,693; NA=6,02∙1023 моль-1; M=204г∙моль-1, получаем А0=(0,2∙103/204)∙(0,693/3,5∙105)∙6,02∙1023=1,2∙1018Бк.
Учитывая, что е=2,72; t=150сут=150сут∙24ч∙3600с=12960000с.
А=1,2∙1018∙2,72-(0,693/345600)∙12960000=6,1∙106Бк.
Задача 5. Оценить эквивалентную дозу, получаемую за счет внешнего γ-облучения за месяц нахождения на территории с уровнем поверхностной активности 137Cs 30Ku/км2.
Теория. Для характеристики радиоактивных излучений и их воздействия на облучаемый объект вводят дозиметрические величины.
Экспозиционная доза X — величина, численно равная отношению суммарного заряда dQ всех ионов одного знака, образовавшихся под действием фотонного излучения в элементарном объеме сухого воздуха, к массе этого объема dm:  . Единица экспозиционной дозы в СИ — кулон на килограмм (Кл/кг). Широко используемой до настоящего времени внесистемной единицей является рентген (Р). 1Р = 2,58∙10
. Единица экспозиционной дозы в СИ — кулон на килограмм (Кл/кг). Широко используемой до настоящего времени внесистемной единицей является рентген (Р). 1Р = 2,58∙10  Кл/кг; 1 Кл/кг = 3876 Р.
Кл/кг; 1 Кл/кг = 3876 Р.
Поглощавшая доза D - энергия излучения, переданная единице массы вещества:  , где dE — энергия, переданная излучением веществу массой dm. Единица поглощенной дозы в СИ - грей (Гр). Один грей - это такая доза, при которой в веществе массой 1 кг поглощается энергия радиоактивных излучений 1 Дж: 1 Гр = 1 Дж/1 кг. Внесистемной единицей поглощенной дозы является рад: 1рад=
, где dE — энергия, переданная излучением веществу массой dm. Единица поглощенной дозы в СИ - грей (Гр). Один грей - это такая доза, при которой в веществе массой 1 кг поглощается энергия радиоактивных излучений 1 Дж: 1 Гр = 1 Дж/1 кг. Внесистемной единицей поглощенной дозы является рад: 1рад=  1Гр=100рад.
1Гр=100рад.
Экспозиционной дозе в 1 Р соответствует поглощаемая биологическими объектами доза, приблизительно равная 0,01 Гр = 1 рад.
Эквивалентная доза Н - произведение поглощенной дозы на коэффициент качества излучения К: H=K∙D. При облучении смешанным излучением эквивалентная доза определяется как сумма произведений поглощенных доз D  от отдельных видов излучений на соответствующие этим излучениям коэффициенты качества К
от отдельных видов излучений на соответствующие этим излучениям коэффициенты качества К  :
:  .
.
Значения коэффициентов качества излучений приведены в Таблице 1.
Таблица 1.
Коэффициенты качества излучения К
| Вид излучения | К,Зв/Гр |
| Рентгеновское и гамма— излучение | |
| Бета — излучение | |
| Альфа — излучение с энергией меньше 10 МэВ | |
| Нейтроны с энергией меньше 20 КэВ | |
| Нейтроны с энергией 0,1 — 10 МэВ | |
| Протоны с энергией меньше 10 МэВ | |
| Тяжелые ядра отдачи |
Единица эквивалентной дозы в СИ — зиверт (Зв). Один зиверт – это такая эквивалентная доза, которая производит такой же биологический эффект, как и поглощенная доза в 1 Гр рентгеновского или гамма -излучения. Внесистемная единица эквивалентной дозы — биологический эквивалент рентгена -бэр. 1 Зв = 100 бэр.
Эффективная эквивалентная доза Н  — сумма произведений эквивалентных доз Н
— сумма произведений эквивалентных доз Н  полученных отдельными органами человека на соответствующие этим органам коэффициенты радиационного риска
полученных отдельными органами человека на соответствующие этим органам коэффициенты радиационного риска  ( (взвешивающие коэффициенты):
( (взвешивающие коэффициенты):  .
.
Значения коэффициентов радиационного риска  приведены в Таблице 2.
приведены в Таблице 2.
Таблица 2
Коэффициенты радиационного риска 
| Орган или ткань |  |
| Яичники или семенники | 0,25 |
| Молочные железы | 0.15 |
| Красный костный мозг | 0.12 |
| Легкие | 0.12 |
| Щитовидная железа | 0.03 |
| Костная ткань | 0.03 |
| Остальные ткани | 0.3 |
| Организм в целом | 1.0 |
Эффективная эквивалентная доза измеряется в тех же единицах, что и эквивалентная.
Мощность дозы излучения — отношение приращения дозы dД ионизирующего излучения к интервалу времени dt, за который это увеличение произошло:  .
.
Мощность экспозиционной дозы:  .
.
Мощность поглощенной дозы:  .
.
Единица измерения мощности экспозиционной дозы в СИ — ампер на килограмм (А/кг или Кл/(кг∙с)). Широко употребляются внесистемные единицы мР/час, мкР/час.
Единица измерения мощности поглощенной дозы излучения — грей в секунду (Гр/с), единица измерения мощности эквивалентной дозы — зиверт а секунду (Зв/с).
С помощью приборов (дозиметров) можно измерить экспозиционную дозу, а также при определенных условиях — поглощенную дозу. Все остальные дозы приборами не измеряются, а могут быть только рассчитаны или оценены по известным радиометрическим величинам или экспозиционной дозе. Для этого необходимо знать переходные коэффициенты. Для внешнего гамма—облучения в условиях нашей республики это следующие коэффициенты: 1 Бк/м2 приводит к эквивалентной дозе 0,022 мкЗв/год, 1 Ku/км2 приводит к эквивалентной дозе 0,8 мЗв/год, 1 мкР/час приводит к эквивалентной дозе 0,05 мЗв/год.
Решение. Переходной коэффициент от уровня поверхностной активности к эквивалентной дозе за счет внешнего γ—облучения – 0,8 мЗв/год на 1 Кu/км2. Следовательно, при уровне поверхностной активности 30 Ku/км2 эквивалентная доза за год составит 0,8x30 = 24мЗв. Доза за месяц будет в 12 раз меньше: 24/12=2мЗв.
Задачи для СРС
Задача 1. В какое ядро превратится ядро (см. Таблицу 3, колонку 1), испустив (см. колонку 2)-частицу? Записать уравнение ядерной реакции.
Задача 2. За какое время распадется 70% начального количества радионуклида (см. колонку 1)? T1/2 радионуклида принять равным (см. колонку 3).
∆N=N0-N= N0∙(1 - ℮-λt); ∆N/N=1 - ℮-λt; ℮-λt=1 - ∆N/N; -λ∙t∙ln ℮=ln (1 - ∆N/N); -λ∙t=(ln (1 - ∆N/N))/ ln ℮; t=((ln (1 - ∆N/N))/ ln ℮) /-λ.
Задача 3. Чугунная плита снизит интенсивность узкого пучка γ-квантов в 10 раз. Во сколько раз снизит интенсивность этого пучка свинцовая плита такой же толщины? Принять линейные коэффициенты ослабления, равные для чугуна (см. колонку 4) и для свинца (см. колонку 5).
n=n0∙℮-µх; n/n= (n0/n)∙℮-µх; 1=(n0/n)∙℮-µх; n0/n=1/℮-µх;ln n0/n=ln 1- (-µх) ∙ ln ℮=0+µх ∙ ln ℮; ln n0/n=µх ∙ ln ℮; µх=(ln n0/n) / ln ℮; х= ((ln n0/n) / ln ℮)/µ.
Задача 4. Определить массу радиоактивного препарата (колонка 1, с Т1/2 – 3 колонка) с начальной активностью, равной начальной активности радионуклида (колонка 6, с Т1/2 – 7 колонка) массой 2 мг.
Задача 5. Оценить эквивалентную дозу, полученную за счет внешнего γ-облучения за год проживания на территории с уровнем поверхностной активности 137Cs (колонка 8).
Таблица 3.
Варианты заданий для самостоятельной работы (соответствуют Вашему номеру)
| N | радионуклид | тип распада | Т1/2 | лин. коэф. ослабл., см-1 | радионуклид | Т1/2 | ур. пов. акт., Ku/км2 | |
| Rb-79 | β+ | 23 мин | 0,11 | 0,3 | Pm-147 | 3 года | 1,2 | |
| Rb-84 | β- | 33 сут | 0,12 | 0,31 | Eu-146 | 5 сут | 1,4 | |
| Cs-130 | β+ | 30 мин | 0,13 | 0,32 | Sm-153 | 47 ч | 1,6 | |
| Cs-132 | β- | 7 сут | 0,14 | 0,33 | Eu-148 | 55 сут | 1,8 | |
| Cs-137 | β- | 30 лет | 0,15 | 0,34 | Eu-152 | 13 лет | ||
| Mn-52 | β+ | 6 сут | 0,16 | 0,35 | Eu-147 | 24 сут | 2,2 | |
| Fr-223 | β- | 22 мин | 0,17 | 0,36 | Gd-151 | 120 сут | 2,4 | |
| Cu-60 | β+ | 23 мин | 0,18 | 0,37 | Tb-160 | 72 сут | 2,6 | |
| Co-58 | β+ | 71 сут | 0,19 | 0,38 | Tm-171 | 2 года | 2,8 | |
| Ag-103 | β+ | 66 мин | 0,2 | 0,39 | Lu-174 | 3 года | ||
| Co-56 | β+ | 79 сут | 0,21 | 0,4 | Th-228 | 2 года | 3,2 | |
| Au-194 | β+ | 40 ч | 0,22 | 0,41 | Th-234 | 24 сут | 3,4 | |
| Au-199 | β- | 3 сут | 0,23 | 0,42 | Pa-230 | 17 сут | 3,6 | |
| Ag-111 | β- | 8 сут | 0,24 | 0,43 | Pa-233 | 27 сут | 3,8 | |
| Mg-28 | β- | 21 ч | 0,25 | 0,44 | U-230 | 21 сут | ||
| Ca-45 | β- | 163 сут | 0,26 | 0,45 | U-232 | 72 года | 4,2 | |
| Sr-89 | β- | 51 сут | 0,27 | 0,46 | U-237 | 7 сут | 4,4 | |
| Sr-90 | β- | 29 лет | 0,28 | 0,47 | Np-235 | 396 сут | 4,6 | |
| Ba-131 | β+ | 12 сут | 0,29 | 0,48 | Np234 | 4 сут | 4,8 | |
| Ba-140 | β- | 13 сут | 0,3 | 0,49 | Np-239 | 2 сут | ||
| Ra-223 | α | 11 сут | 0,31 | 0,5 | Pu-236 | 3 года | 5,2 | |
| Ra-228 | β- | 6 лет | 0,32 | 0,51 | Pu-241 | 14 лет | 5,4 | |
| Zn-65 | β+ | 244 сут | 0,33 | 0,52 | Am-240 | 51 ч | 5,6 | |
| Zn-72 | β- | 47 ч | 0,34 | 0,53 | Cm-244 | 18 лет | 5,8 | |
| Cd-107 | β+ | 7ч | 0,35 | 0,54 | Cm-249 | 64 мин | ||
| Cd-115 | β- | 54 ч | 0,36 | 0,55 | Bk-245 | 5 сут | 6,2 | |
| Hg-193 | β+ | 4 ч | 0,37 | 0,56 | Cf-250 | 13 лет | 6,4 | |
| Hg-203 | β- | 47 сут | 0,38 | 0,57 | Sn-125 | 10 сут | 6,6 | |
| Co-60 | β- | 5 лет | 0,39 | 0,58 | Pb-210 | 22 года | 6,8 | |
| In-109 | β+ | 4 ч | 0,4 | 0,59 | Zr-95 | 64 сут | ||
| Tl-202 | β+ | 12 сут | 0,41 | 0,6 | Hf-181 | 42 сут | 7,2 | |
| Tl-204 | β- | 4 года | 0,42 | 0,61 | P-33 | 25 сут | 7,4 | |
| Sc-46 | β- | 84 сут | 0,43 | 0,62 | As-74 | 18 сут | 7,6 | |
| Y-88 | β+ | 107 сут | 0,44 | 0,63 | Sb125 | 60 сут | 7,8 | |
| Y-91 | β- | 59 сут | 0,45 | 0,64 | Bi-205 | 15 сут | ||
| Ac-225 | α | 10 сут | 0,46 | 0,65 | V-48 | 16 сут | 8,2 | |
| Ac227 | β- | 28 лет | 0,47 | 0,66 | Nb-95 | 35 сут | 8,4 | |
| Ce-141 | β- | 325 сут | 0,48 | 0,67 | Ta-183 | 5 сут | 8,6 | |
| Nd-147 | β- | 11 сут | 0,49 | 0,68 | Po-210 | 138 сут | 8,8 | |
| Pm-147 | β- | 3 года | 0,5 | 0,69 | W-185 | 75 сут | ||
| Eu-146 | β+ | 5 сут | 0,51 | 0,7 | I-126 | 13 сут | 9,2 | |
| Sm-153 | β- | 47 ч | 0,52 | 0,71 | Rb-79 | 23 мин | 9,4 | |
| Eu-148 | α | 55 сут | 0,53 | 0,72 | Rb-84 | 33 сут | 9,6 | |
| Eu-152 | β- | 13 лет | 0,54 | 0,73 | Cs-130 | 30 мин | 9,8 | |
| Eu-147 | β+ | 24 сут | 0,55 | 0,74 | Cs-132 | 7 сут | ||
| Gd-151 | α | 120 сут | 0,56 | 0,75 | Cs-137 | 30 лет | 10,2 | |
| Tb-160 | β- | 72 сут | 0,57 | 0,76 | Mn-52 | 6 сут | 10,4 | |
| Tm-171 | β- | 2 года | 0,58 | 0,77 | Fr-223 | 22 мин | 10,6 | |
| Lu-174 | β+ | 3 года | 0,59 | 0,78 | Cu-60 | 23 мин | 10,8 | |
| Th-228 | α | 2 года | 0,6 | 0,79 | Co-58 | 71 сут | ||
| Th-234 | β- | 24 сут | 0,61 | 0,8 | Ag-103 | 66 мин | 11,2 | |
| Pa-230 | α | 17 сут | 0,62 | 0,4 | Co-56 | 79 сут | 11,4 | |
| Pa-233 | β- | 27 сут | 0,63 | 0,41 | Au-194 | 40 ч | 11,6 | |
| U-230 | α | 21 сут | 0,64 | 0,42 | Au-199 | 3 сут | 11,8 | |
| U-232 | α | 72 года | 0,65 | 0,43 | Ag-111 | 8 сут | ||
| U-237 | β- | 7 сут | 0,66 | 0,44 | Mg-28 | 21 ч | 12,2 | |
| Np-235 | α | 396 сут | 0,67 | 0,45 | Ca-45 | 163 сут | 12,4 | |
| Np234 | β+ | 4 сут | 0,68 | 0,46 | Sr-89 | 51 сут | 12,6 | |
| Np-239 | β- | 2 сут | 0,69 | 0,47 | Sr-90 | 29 лет | 12,8 | |
| Pu-236 | α | 3 года | 0,7 | 0,48 | Ba-131 | 12 сут | ||
| Pu-241 | β- | 14 лет | 0,1 | 0,49 | Ba-140 | 13 сут | 13,2 | |
| Am-240 | α | 51 ч | 0,12 | 0,5 | Ra-223 | 11 сут | 13,4 | |
| Cm-244 | α | 18 лет | 0,13 | 0,51 | Ra-228 | 6 лет | 13,6 | |
| Cm-249 | β- | 64 мин | 0,14 | 0,52 | Zn-65 | 244 сут | 13,8 | |
| Bk-245 | α | 5 сут | 0,15 | 0,53 | Zn-72 | 47 ч | ||
| Cf-250 | α | 13 лет | 0,16 | 0,54 | Cd-107 | 7ч | 14,2 | |
| Sn-125 | β- | 10 сут | 0,17 | 0,55 | Cd-115 | 54 ч | 14,4 | |
| Pb-210 | β- | 22 года | 0,18 | 0,56 | Hg-193 | 4 ч | 14,6 | |
| Zr-95 | β- | 64 сут | 0,19 | 0,57 | Hg-203 | 47 сут | 14,8 | |
| Hf-181 | β- | 42 сут | 0,2 | 0,58 | Co-60 | 5 лет | ||
| P-33 | β- | 25 сут | 0,22 | 0,59 | In-109 | 4 ч | 15,2 | |
| As-74 | β+ | 18 сут | 0,24 | 0,6 | Tl-202 | 12 сут | 15,4 | |
| Sb125 | β- | 60 сут | 0,26 | 0,61 | Tl-204 | 4 года | 15,6 | |
| Bi-205 | β+ | 15 сут | 0,28 | 0,62 | Sc-46 | 84 сут | 15,8 | |
| V-48 | β+ | 16 сут | 0,3 | 0,63 | Y-88 | 107 сут | ||
| Nb-95 | β- | 35 сут | 0,32 | 0,64 | Y-91 | 59 сут | 16,2 | |
| Ta-183 | β- | 5 сут | 0,34 | 0,65 | Ac-225 | 10 сут | 16,4 | |
| Po-210 | α | 138 сут | 0,36 | 0,66 | Ac227 | 28 лет | 16,6 | |
| W-185 | β- | 75 сут | 0,38 | 0,67 | Ce-141 | 325 сут | 16,8 | |
| I-126 | β+ | 13 сут | 0,4 | 0,68 | Nd-147 | 11 сут |




1. Изучение лучевых катаракт на кроликах показало, что под действием γ -излучения катаракты развиваются при дозе D1 = 200 рад. Под действием быстрых нейтронов (залы ускорителей) катаракта возникает при дозе D2 = 20 рад. Определить коэффициент качества для быстрых нейтронов.

2. На сколько градусов увеличится температура фантома (модели человеческого тела) массой 70 кг при дозе γ-излучения Х = 600 Р? Удельная теплоемкость фантома с = 4,2х103 Дж/кг. Считать, что вся полученная энергия идет на нагревание.

3. Человек весом 60 кг в течение 6 ч подвергался действию γ- излучения, мощность которого составляла 30 мкР/час. Считая, что основным поглощающим элементом являются мягкие ткани, найти экспозиционную, поглощенную и эквивалентную дозы облучения. Найти поглощенную энергию излучения в единицах СИ.

4. Известно, что разовая летальная экспозиционная доза для человека равна 400 Р (50 % смертности). Выразить эту дозу во всех других единицах.

6. Мощность экспозиционной дозы γ -излучения на расстоянии r = 0,1 м от точечного источника составляет Nr = 3 Р/час. Определить минимальное расстояние от источника, на котором можно ежедневно работать по 6 ч без защиты. ПД = 20 мЗв/год. Поглощение γ -излучения воздухом не учитывать.
Решение (требуется аккуратное выравнивание единиц измерения) По нормам радиационной безопасности эквивалентная доза, полученная за год работы, составляет Н = 20 мЗв. Коэффициент качества для γ -излучения К = 1.
Примеры решения задач Задача 1. Рассчитать суммарную активность трития, образовавшегося в результате испытания ядерного оружия до 1970 г., если общий эквивалент ядерных взрывов составил 220 Мт. Решение. Образование трития при испытании ядерного оружия составляет 2.6*1013 Бк/Мт. До 1970 г. общий эквивалент ядерных взрывов составил 220 Мт. Образование трития: 220 Мт·2.б·1013 Бк/Мт = 5.7·1015 Бк.
По санитарным нормам допустимая плотность потока быстрых нейтронов составляет: I0 = 20 n·см-2·с-1. Определить на каком минимальном расстоянии от источника, интенсивностью S = 106 n/с, можно работать без дополнительной защиты.
Минимальное безопасное расстояние из соотношения (1):
Индивидуальная доза облучения, полученная в результате воздействия источника 60Со в течении 10 с, составила 100 Гр. Сколько фотонов γ-излучения попало при этом в организм человека, если каждый фотон теряет в тканях тела около 40 % своей энергии?
Для человека весом 75 кг поглощенная доза от одной пары фотонов составит
При получении дозы 100 Гр число фотонов, попавших в организм, составит
Студент предполагает использовать источником 90Sr, имеющим активность А = 270 МБк и содержащимся в стеклянной пробирке, в качестве защиты только плотные перчатки.
Предельно допустимая доза: Работать опасно!!!
Количество 90Sr, которое ежедневно попадает с пищей в организм человека, составляет 0.94 Бк. Каково значение дозы, накопленной в костной ткани за год?
2) Будем считать, что в организме поглощается 10% фотонов. Общее количество энергии, поглощенной в организме от одного распада: Q = (0.546+2.27)·0.4 + 1.734·0.1 = 1.3 МэВ = Фрагмент таблицы 32.
Таким образом, в сутки костная ткань поглощает Q=2.08·10-13 Дж·5.68·104=11.8Дж. Доза, поглощенная в год: 365·1.88*10-9 Дж = 4.3·10-6 Дж. Доза, поглощенная за год в 1 кг костной ткани:
В организм человека попало 10 мг 55Fe. Найти значение поглощенной дозы за 10-летний период. Период полураспада 55Fе =-2.9 года. Q=0.22 МэВ.
Из 10 мг за 10 лет распалось 10 - 0.926=9.074 мг.
Количество выделившейся энергии: Q=0.22·0.99·1020=2.19·1019 МэВ=3.50·10б Дж. Чтобы найти энергию, отнесенную к единице массы, предположим, что облучается примерно 1/3 часть тела весом 75 кг, т.е. 25 кг. Тогда:
Каково максимальное количество радионуклида 90Sr при попадании которого в организм не будет превышена доза Д =1 мГр/год. T1/2(90Sr) = 28 лет. Решение.
Доля ядер радионуклида 90Sr, распадающаяся за год: K = N/N0 = 1 − exp(−0.693/T1/2) = 1 − e−(0.693/28) = 2.5·10−2 Используя схему распада радиоактивного изотопа 90Sr, получим энергию, выделяющуюся в костях на один акт распада: Е* = 0.1·Eγ + 0.4· Полное число ядер изотопа:
Какова поглощенная доза в организме человека в течении 10 лет, если через органы дыхания в него попало 100 мкг изотопа 239Pu? Период полураспада 239Pu равен 2.4·104 лет.
Число ядер 239Pu распавпшхся за 10 лет:
Распад 239Pu приводит к появлению трех
При какой концентрации плутония в воздухе n годовая доза от его попадания в легкие составит Д = 1.7·10-6 Гр. Решение.
где N(t) - число ядер 239Pu в момент времени t.
Учитывая, что вследствии большого периода полураспада вторым членом в (2) можно пренебречь, после интегрирования (2) получим:
Из (3) и (1) получим число ядер распавшихся за время t: dNp (t) =
Энергия Е, поглощенная в ткани легких за год: E = Д МЛ = 1.7·10-6 · 0.5 = 8.5·10-7 Дж. Число распадов ядер, необходимое для выделения энергии Е:
Из (4) получим концентрацию 239Pu в воздухе:
|
 2017-11-01
2017-11-01 13635
13635




 -распада составляют
-распада составляют  0.3-0.4 от
0.3-0.4 от  .
.

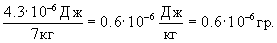


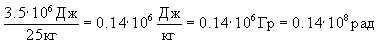
 =0.7 (табл. 32). Поэтому полная энергия, выделенная в организме за год, будет составлять:
=0.7 (табл. 32). Поэтому полная энергия, выделенная в организме за год, будет составлять:



 -линий при энергиях Eα и с вероятностями распада, указанными в таблице.
-линий при энергиях Eα и с вероятностями распада, указанными в таблице. α = 5.1 МэВ. Масса тела М = 70 кг. Поглощенная доза:
α = 5.1 МэВ. Масса тела М = 70 кг. Поглощенная доза:
 = 0.5 кг. Число актов распада 239Pu за время dt:
= 0.5 кг. Число актов распада 239Pu за время dt: N(t)dt
N(t)dt