Определение ускорения при естественном способе задания ее движения. (стр 51-54)

Постановка задачи.

Пусть известны:

1. траектория движения точки АВ.

2. начало отсчета и положительное направление отсчета дуговой координаты s.

3. закон движения по траектории s = s(t)

Определить ускорение точки по модулю и направлению.

 

Запишем исходные формулы ускорения и скорости:

=

 

= ,

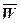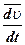
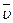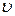
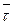где 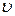алгебраическая скорость точки, а 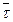единичный орт.

Подставим в первую формулу вектор скорости, т. е продифференцируем данное произведение. Необходимо учесть, что скорость меняется (движение может быть неравномерным), а вектор 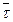модуль которого равняется единице переменный по направлению, но постоянный по значению. Поэтому придется продифференцировать оба множителя. Дифференцируем как произведение.

= ( )

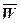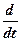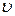
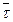Дифференцируем как произведение.

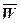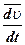
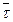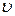
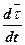= + (9)

Вектор 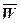мы представили в виде двух составляющих.

Вектор 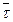-показывает, что первое слагаемое направлено по касательной, а второй вектор показывает направление по нормали.

Дальше необходимы знания дифференциальной геометрии. Необходимо рассмотреть формулы ФРЭНЕ.

Запишем формулу без вывода.

Можно доказать следующее выражение:

=

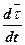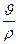
И тогда ускорение можно записать:

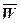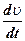
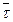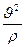
= + (10)

Данная формула показывает разложение вектора ускорения по естественным осям координат.

Введем следующие обозначения:

W_τ = 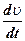- касательная составляющая ускорения

W_n = 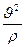- нормальная составляющая ускорения

W_b = 0 - составляющая по бинормали

 

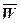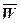= _τ + 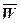_n (11)

 

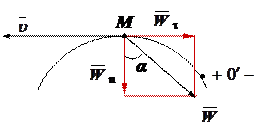
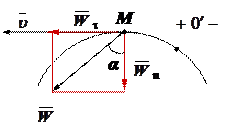
Вектор ускорения точки равен геометрической сумме касательной и нормальной составляющих.

Вектор ускорения, находиться в соприкасающейся плоскости и всегда направлен в сторону вогнутости траектории.

 

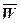_n – всегда направлен по главной нормали к центру кривизны траектории.

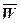_τ - направлен по касательной к траектории в сторону скорости при ускоренном движении, и в противоположном, если движение замедленно.

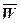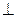
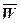_{τ n}

 

Из равенства (11) заключаем, что полное ускорение 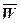всегда находиться в соприкасающейся плоскости.

 

 

 

 

Касательное ускорение возникает при неравномерном движении и характеризует изменение скорости по модулю.

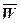_n = 0 - при прямолинейном движении.

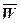_n 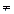0 - при криволинейном движении

Модуль ускорения рассчитываем по следующей формуле

 

W =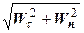

Ориентация вектора скорости в пространстве характеризуется направляющими косинусами.

cos ( ; ) =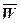

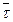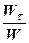
cos ( ; ) =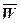

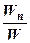
Самостоятельно стр 54 – 63