Характеристика составляющих временного ряда

Временные ряды

При построении эконометрической модели используются два типа данных:

1) данные, характеризующие совокупность различных объектов в определенный момент времени;

2) данные, характеризующие один объект за ряд последовательных моментов времени.

Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов.

При анализе многих экономических показателей часто используются ежегодные, ежеквартальные, ежемесячные, ежедневные данные. Для рационального анализа необходимо систематизировать моменты получения соответствующих статистических данных.

В этом случае следует упорядочить данные по времени их получения и построить так называемые временные ряды.

Временной ряд (ряд динамики) – это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:

1) факторы, формирующие тенденцию ряда;

2) факторы, формирующие циклические колебания ряда;

3) случайные факторы.

Рассмотрим воздействие каждого фактора на временной ряд в отдельности.

Большинство временных рядов экономических показателей имеют тенденцию, характеризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. Все эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель. Однако в совокупности они формируют его возрастающую или убывающую тенденцию.

Также изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку экономическая деятельность ряда отраслей экономики зависит от времени года. При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктуры рынка.

Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты.

Реальные данные чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.

В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

Аддитивная модель имеет вид:

(4.1)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой сезонной и случайной 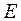компонент.

Мультипликативная модель имеет вид:

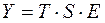(4.2)

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой , сезонной и случайной 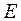компонент.

Пусть исследуется показатель Его значение в текущий момент (период) времени обозначают ; значения в последующие моменты обозначаются ; значения в предыдущие моменты времени обозначаются .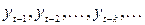

При изучении зависимостей между такими показателями либо при анализе их развития во времени в качестве объясняющих переменных используются не только текущие значения переменных, но и некоторые предыдущие по времени значения, а также само время . Модели такого типа называются динамическими.

В свою очередь переменные, влияние которых характеризуется определенным запаздыванием, называются лаговыми переменными.

Обычно динамические модели подразделяются на два класса:

1) модели с лагами (модели с распределенными лагами) – содержат в качестве лаговых переменных лишь независимые (объясняющие) переменные. Примером является модель:

(4.3)