Лекції 3-4. Елементи загальної теорії систем

Визначення систем:

1) Система – сукупність деяких об’єктів та зв’язків між ними (визначення сформулював біолог Берталампфі у 1920р.)

2) Система – сукупність взаємопов’язаних елементів, що розглядається як єдина структура, має певні властивості та розвивається за деякими законами.

3) Система -формальний взаємозв’язок між ознаками, що спостерігаються, і властивостями (М.Месарович).

4) Системою називається деяка власна підмножина власних висловлювань (вербальне визначення системи за М.Месаровичем).

5) Визначення системи в теорії множин (М. Месарович)

Загальною системою називається відношення на непустих (абстрактних) множинах

S 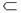{V_i: і є І}, де

· – декартовий добуток;

І – множина індексів;

V_i – об’єкт системи (властивості або стани).

Якщо І скінчена, тоді система представляється у вигляді:

S 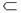V₁ V₂ V₃ ……. V_n

 

Визначення «чорної скриньки».

Нехай І _х 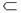І (І _х - підмножина І) та І_Y 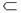утворюють розбиття множини І, тобто нехай І _х ∩ І _у= ø та І _х 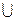І_Y = І, тоді:

множина Х = { V _i: і є І_x } – вхідний об’єкт

множина Y = { V _i: і є І_Y} – вихідний об’єкт системи.

Тоді система S визначається відношенням:

S 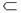X Y

Такі системи називаються системами «вхід-вихід» або «чорними скриньками».

Для нас неважливі процеси, що проходять усередині системи, ми розглядаємо її як об’єкт, що має деякі входи і деякі виходи, ігноруючи внутрішню структуру.

Приклад: Прикладом системи «чорна скринька» може служити S – деяка мікросхема, що має один вхід і один вихід:

Х ={0,1} Y ={0,1}   X Y= {00,01,10,11}

 

 

Системи поділяються на 2 класи.

1. Функціональні (системи однозначної відповідності).

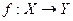
де f – функція, яка кожному елементу множини Х за деяким законом ставить у відповідність один і тільки один елемент множини Y.

 

2. Динамічні системи.

Визначення М.Месаровича:

Система S 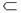X Y називається динамічною тоді і тільки тоді, коли знайдуться два таких сімейства відображень

та

таких, що:

1) сімейство 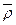узгоджується з S, тобто є сімейством реакції цієї системи.

2) усі функції з сімейства 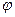задовольняють таким умовам:

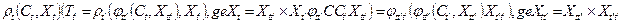
де 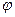- сімейство функцій переходів станів.

 

При визначенні динамічної системи існують 3 основні кроки:

1. Задаються X,Y,Z, де

X – простір входів;

Y – простір виходів;

Z – простір станів.

Система в любий час знаходиться в деякому стані (властивість системи):

2. Задається 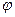; функція переходів з одного стану в інший:

Таким чином, наступний стан залежить від попереднього та вхідного сигналу.

3. Задається функція виходів :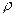

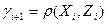
Таким чином, вихідний сигнал залежить від стану системи та вхідного сигналу.

Приклад динамічної системи – система регулювання рівня води (система з гістерезісом) наведена на рис.3.1.

 

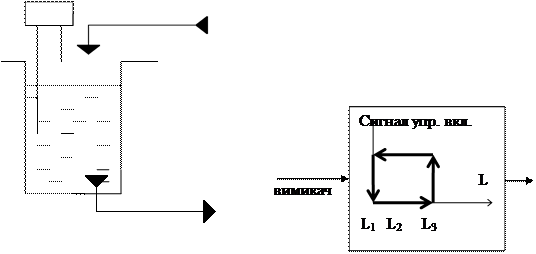Рис.3.1. Система регулювання рівня води

 

В стані L₂ можливі два значення виходу – тобто наведена залежність між сигналом управління і рівнем води не є функцією, а, навпаки, являє собою приклад найпростішої динамічної системи.