2017-11-01
367
А) Интегрирование простейших дробей
Опр. Элементарными или простейшими называются правильные дроби следующего вида:
I. 
;
II. 
;
III. 
где квадратный трехчлен 
не имеет действ. корней;
IV. 
, где квадратный трехчлен не имеет действ. корней.
Во всех четырех случаях: 
.
Далее приведем формулы для интегрирования дробей I и II типов (они после линейной замене являются табличными), интегрирование дробей типа III рассмотрим на примерах, тип IV рассматривать не будем.
.
Рассмотрим сначала интегрирование дробей вида 
где квадратный трехчлен не имеет действ. корней. Это производится с помощью выделения полного квадрата в знаменателе и сведения к табличному интегралу №9 
.
Пр. 
.
Теперь полностью рассмотрим интегрирование простейших дробей третьего типа. Для этого сначала в числителе дроби выделяется производная знаменателя, а затем интеграл раскладывается в сумму двух интегралов. Первый решается с помощью замены, второй – только что рассмотренным способом.
Пр. 
.
Замечание: Интегралы вида 
вычисляются так же, как и интеграл от простейшей дроби третьего типа, только сводится к табличным интегралам 
или 
.
Пр. 
(выделим в числителе производную подкоренного выражения) 
.
В) Интегрирование дробей с помощью разложения на простейшие
Вспомним некоторые факты из теории многочленов:
Любой многочлен может быть разложен в произведение линейных сомножителей и квадратных, не имеющих действительных корней, т.е. 
.
Рассмотрим более простой случай: Пусть имеется правильная дробь вида 
и 
, тогда существуют 
, такие что:
. Нахождение такого разложения производится методом неопределенных коэффициентов.
Итак:
1) правильную дробь методом неопределенных коэффициентов раскладываем в сумму простейших, интегрирование которых уже описано;
2) в случае неправильной дроби сначала выделяем целую часть (разделив числитель на знаменатель), а затем раскладываем правильный остаток на простейшие.
Пр. Разложить на простейшие дроби: 
.
, отсюда получаем: 
, т.е. 
Пр. 
.
Пр. 
.
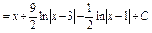Всякая правильная дробь разлагается единственным образом на сумму простейших:
Случай 1.
В разложение знаменателя входят только множители первой степени и ни один из них не повторяется. Тогда правильная дробь разлагается на простейшие по формуле 
, (*)
где А, В, …L находятся по методу неопределенных коэффициентов.
Случай 2.
В разложение знаменателя входят лишь множители первой степени и некоторые из них повторяются. Пусть множитель 
повторяется k раз. Тогда в разложении (*) надо заменить соответствующие k одинаковых членов суммой простейших дробей вида 
. Аналогично для других повторяющихся множителей. Простейшие дроби, отвечающие неповторяющимся множителям, остаются прежними. Постоянные, входящие в разложение, определяются, как и в случае 1.
Случай 3.
В разложение знаменателя входят множители второй степени (неразложимые на действительные множители первой степени), и ни один из них не повторяется. Тогда в разложении дроби каждому множителю 
соответствует простейшая дробь 
(типа III). Множителям первой степени (если они есть) по-прежнему соответствуют простейшие дроби типа I или II.
Случай 4.
В разложение знаменателя входят множители второй степени (неразложимые на действительные множители первой степени), и некоторые из них повторяются. Тогда в разложении дроби каждому множителю 
, повторяющемуся k раз, соответствует сумма простейших дробей вида
.
