Интегрирование некоторых иррациональных функций

1. Интегралы вида вычисляются выделением полного квадрата из квадратного трехчлена и последующей подстановкой .
2. Интегралы вида , где R – рациональная функция, находятся с помощью подстановки , где n – наименьшее общее кратное , .
3. Интегралы вида , где R – рациональная функция, находятся подстановкой ,

интегралы вида находятся подстановкой ,

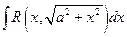интегралы вида находятся подстановкой .

Таблица основных интегралов

; ; . ;

; ; ; ;

;

Метод интегрирования по частям

Практика показывает, что большую часть интегралов, вычисляемых интегрированием по частям, можно разбить на три группы:

1. К первой группе относятся интегралы вида: , , 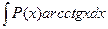, , , где Р(х) – многочлен. Для их вычисления следует положить u равным одной из указанных функций, а .
2. Ко второй группе относятся интегралы вида , , , где Р(х) – многочлен, а k – некоторое число. Для вычисления следует положить u= Р(х), а 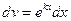, , соответственно.
3. К третьей группе относятся интегралы вида , , 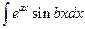где а и b – некоторые числа. Эти интегралы вычисляются двукратным интегрированием по частям.