Изучение гармонических колебаний математического и физического маятников

Различные механические колебания широко распространены в окружающем мире, в технике и быту. Простейшей моделью колебательной системы является математический маятник – подвешенное на тонкой нерастяжимой нити или на тонком стержне длиной тело размером гораздо меньшим и потому принимаемое за материальную точку. Массы нити или стержня считаются пренебрежимо малыми по сравнению с массой тела .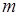

Физическим маятником называют твердое тело, которое может вращаться вокруг неподвижной горизонтальной оси О - оси вращения (качания) маятника, не проходящей через центр тяжести тела (рис. 8.1).

Законом движения физического маятника является уравнение динамики вращательного движения твердого тела вокруг оси вращения

, (8.1)

где I – момент инерции маятника относительно оси вращения, – угол отклонения маятника, вектора угла , бесконечно малого поворота , угловой скорости и углового ускорения направлены вдоль оси вращения , , , - проекции этих векторов на ось , - время, – вращающий момент, - проекция момента на ось , – сила тяжести, приложенная к центру масс С и вызывающая повороты маятника, L – расстояние между осью вращения и центром масс маятника С.

Момент инерции I материальной точки массой 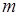, находящейся на расстоянии от оси равен

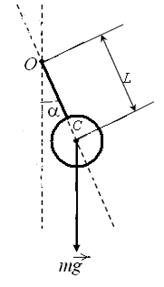
, (8.2)

Согласно закону аддитивности моментов инерции, момент инерции сложной системы тел равен сумме моментов инерции частей, составляющих данную систему. Поэтому момент инерции I твердого тела с плотностью относительно некоторой оси определяется выражением

, (8.3)

где – расстояние элемента массы от оси вращения. Для нахождения момента инерции тел относительно произвольной оси используется теорема Гюйгенса[1] – Штейнера. Согласно этой теореме момент инерции 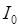тела относительно оси, проходящей через центр масс, и момент инерции относительно второй оси, параллельной первой, и удаленной от нее на расстоянии , связаны соотношением

. (8.4)

При выборе на рис. 8.1 положительного направления отсчета углов поворота против часовой стрелки вектор направлен из плоскости чертежа вдоль оси вращения: вертикально вверх (к нам) при и вертикально вниз (от нас) при 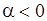. На рис. 8.1 показано отклонение маятника с , при котором вектор вращающего момента направлен из плоскости чертежа вертикально вниз (от нас). При 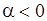он будет направлен противоположно. Поэтому вектора и всегда направлены противоположно друг другу. Выберем направление оси из плоскости чертежа вдоль оси вращения вертикально вверх (к нам) и обозначим , при этом . Запишем уравнение (8.1) в проекции на ось

. (8.5)

При малых отклонениях маятника из положения равновесия и . Вращающий момент , стремящийся вернуть маятник в положение равновесия, пропорционален углу отклонения (с противоположным знаком) и в этом отношении аналогичен упругой силе. Тогда уравнение (8.5) примет вид

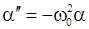, , (8.6)

а его решение является уравнением гармонических колебаний

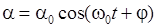, (8.7)

с амплитудой , циклической частотой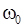

(8.8)

и периодом

. (8.9)

Математический маятник, подвешенный на тонком стержне (нити), является частным случаем физического маятника с и моментом инерции . В этом случае формулы (8.8), (8.9) переходят в формулы

, (8.10)

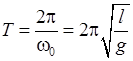. (8.11)

Формула (8.11) позволяет определять ускорение свободного падения по измерениям периода колебаний маятника :

. (8.12)

Формула (8.9) позволяет определять момент инерции или его отношение к массе по измерениям периода колебаний маятника :

. (8.13)

Кинетическая энергия физического маятника в ходе его колебаний меняется по закону

, (8.14)

где – угловая скорость. За нулевое значение потенциальной энергии маятника примем его потенциальную энергию при нулевом отклонении . Высота подъема центра масс тела с учетом приближенной формулы при 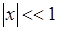равна

. (8.15)

Потенциальная энергия маятника равна

. (8.16)

В предыдущих рассуждений предполагалось отсутствие трения, в таком случае в ходе колебаний по закону (8.7) полная механическая энергия физического маятника сохраняется

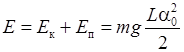. (8.17)

Физические маятники №1 и №2, применяемые в настоящей работе, представляет собой сплошные однородные шары на нити длиной . Пренебрегая массой нити, можно считать, что центр масс маятника находится в центре шара. Расстояние L от центра тяжести до точки подвеса равно 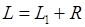. Для однородного шара радиуса и массы 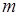момент инерции 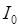относительно оси, проходящей через его центр масс, равен

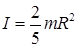. (8.18)

Момент инерции шара относительно оси, проходящей через точку подвеса, можно вычислить по теореме Гюйгенса-Штейнера:

. (8.19)

Физический маятник №3, применяемый в настоящей работе, представляет собой тонкостенную сферу радиуса (шарик для настольного тенниса) на нити длиной 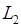. Пренебрегая массой нити, можно считать, что центр масс маятника находится в центре шара. Расстояние L от центра тяжести до точки подвеса равно . Для тонкого кольца радиуса и массы 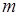момент инерции 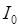относительно оси, совпадающей с его диаметром равен

. (8.20)

Тонкостенную сферу радиуса и массы 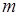можно представить состоящей из множества колец и ее момент инерции 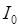относительно оси, проходящей через центр масс, равен

. (8.21)